第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. (3分)(2025·南通崇川区)下列说法正确的是(
A.顶点在圆上的角是圆周角
B.两边都和圆相交的角是圆周角
C.圆心角是圆周角的2倍
D.圆周角度数等于它所对的弧所对的圆心角度数的一半
D
)A.顶点在圆上的角是圆周角
B.两边都和圆相交的角是圆周角
C.圆心角是圆周角的2倍
D.圆周角度数等于它所对的弧所对的圆心角度数的一半
答案:
D
2. (3分)如图,$\triangle ABC的顶点A$,$B$,$C均在\odot O$上,若$\angle ABC+\angle AOC= 90^{\circ}$,则$\angle AOC$的度数为(
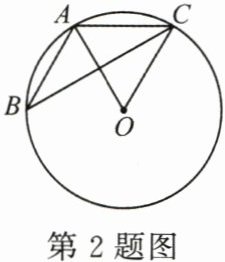
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$70^{\circ}$
C
)
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$70^{\circ}$
答案:
C
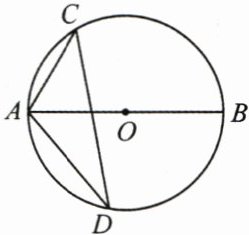
3. (3分)如图,$AB是\odot O$的直径,$C$,$D$为圆上两点,$\angle AOC= 130^{\circ}$,则$\angle D$的度数为
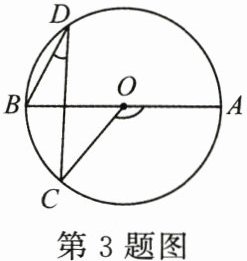
25°
.
答案:
25°
4. (3分)(2025·德州庆云县质检)如图,$A$,$B$,$C是\odot O$上的三点,$\angle CAO= 25^{\circ}$,$\angle BCO= 35^{\circ}$,则$\angle AOB$的度数为______.
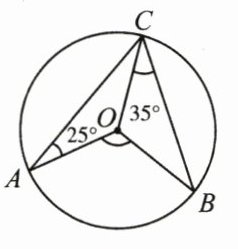

120°
答案:
120°
5. (3分)如图,图中相等的圆周角有(
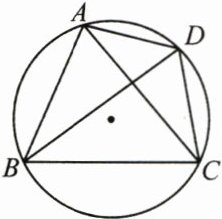
A.3对
B.4对
C.5对
D.6对
B
)
A.3对
B.4对
C.5对
D.6对
答案:
B
6. (3分)(2025·宣城质检)如图,$AB是\odot O$的直径,点$C在\odot O$上,$\angle BAC= 30^{\circ}$,点$P在线段OB$上运动,设$\angle ACP= x^{\circ}$,则$x$的取值范围是(
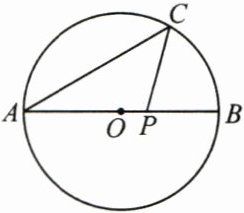
A.$x\leqslant90$
B.$x>30$
C.$30<x<90$
D.$30\leqslant x\leqslant90$
D
)
A.$x\leqslant90$
B.$x>30$
C.$30<x<90$
D.$30\leqslant x\leqslant90$
答案:
D
7. (3分)(2025·北京海淀区月考)如图,在$\odot O$中,$AB$是直径,弦$AC$的长为5cm,点$D$在圆上,且$\angle ADC= 30^{\circ}$,则$\odot O$的半径为
5
cm.
答案:
5
8. (6分)已知$AB为\odot O$的直径,弦$BE= DE$,$AD$,$BE的延长线交于点C$.求证:$AC= AB$.


答案:
证明:如图,连接 AE.

∵AB 为⊙O 的直径,
∴∠AEB=90°.
∴∠AEB=∠AEC=90°.
∵BE=DE,
∴$\overset{\frown}{DE}=\overset{\frown}{BE}$.
∴∠DAE=∠BAE.
∵∠C=90°-∠DAE,∠B=90°-∠BAE,
∴∠B=∠C.
∴AC=AB.
证明:如图,连接 AE.

∵AB 为⊙O 的直径,
∴∠AEB=90°.
∴∠AEB=∠AEC=90°.
∵BE=DE,
∴$\overset{\frown}{DE}=\overset{\frown}{BE}$.
∴∠DAE=∠BAE.
∵∠C=90°-∠DAE,∠B=90°-∠BAE,
∴∠B=∠C.
∴AC=AB.
查看更多完整答案,请扫码查看


