《2025年初中同步练习册分层卷九年级数学上册人教版》

9. (3 分)(2025·邢台质检)已知实数 $ a $,$ b $ 满足 $ b - a = 1 $,则代数式 $ a^2 + 2b - 6a + 7 $ 的最小值等于 (A)
A.5
B.4
C.3
D.2

答案： A

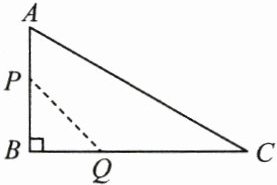
10. (3 分)如图,在 $ \triangle ABC $ 中,$ \angle B = 90° $,$ AB = 6 cm $,$ BC = 12 cm $,动点 $ P $ 从点 $ A $ 开始沿边 $ AB $ 向点 $ B $ 以 $ 1 cm/s $ 的速度移动(不与点 $ B $ 重合),动点 $ Q $ 从点 $ B $ 开始沿边 $ BC $ 向点 $ C $ 以 $ 2 cm/s $ 的速度移动(不与点 $ C $ 重合).如果点 $ P $,$ Q $ 分别从点 $ A $,$ B $ 同时出发,那么经过 3s,四边形 $ APQC $ 的面积最小。

答案： 3

11. (3 分)(2025·济南市中区质检)已知函数 $ y = mx^2 + 2mx + 1 $ 在 $ -3 \leq x \leq 2 $ 上有最大值 4,则常数 $ m $ 的值为 -3或$\frac{3}{8}$。

答案： -3或$\frac{3}{8}$ 解析：由题知，抛物线的对称轴为直线x=-1.
当m＞0时，抛物线开口向上，又-3≤x≤2，则当x=2时，函数取得最大值.
因为函数的最大值为4，则2²m+2×2m+1=4，解得m=$\frac{3}{8}$.
当m＜0时，抛物线开口向下，因为-3≤x≤2，则当x=-1时，函数取得最大值.
因为函数的最大值为4，则(-1)²m+(-1)×2m+1=4，解得m=-3.
综上所述，m的值为-3或$\frac{3}{8}$.

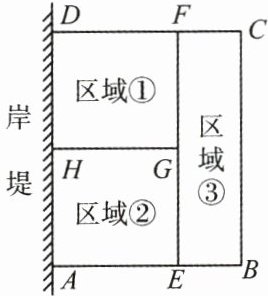
12. (9 分)为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为 160 m 的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设 $ BC $ 的长度为 $ x m $,矩形区域 $ ABCD $ 的面积为 $ y m^2 $。
(1)是否存在 $ x $ 的值,使得矩形 $ ABCD $ 的面积是 $ 1500 m^2 $？请说明理由。
(2)$ x $ 为何值时,$ y $ 有最大值？最大面积是多少？

答案： 解：
(1)设AE=a m.
由题意，得AE·AD=2BE·BC.
∵AD=BC，
∴BE=$\frac{1}{2}$a m，AB=$\frac{3}{2}$a m.
由题意，得2x+3a+2×$\frac{1}{2}$a=160，
∴a=40-$\frac{1}{2}$x.
∵a＞0，
∴40-$\frac{1}{2}$x＞0，即x＜80.
由题意，得y=AB·BC=$\frac{3}{2}$ax=$\frac{3}{2}$(40-$\frac{1}{2}$x)x.
∴y=-$\frac{3}{4}$x²+60x(0＜x＜80).
令y=1500，得-$\frac{3}{4}$x²+60x=1500.
化简，得x²-80x+2000=0.
∵Δ=80²-4×2000=6400-8000＜0，
∴方程无解.
故不存在x的值，使得矩形ABCD的面积是1500m².
(2)
∵y=-$\frac{3}{4}$x²+60x=-$\frac{3}{4}$(x-40)²+1200，
∴当x=40时，y有最大值，最大面积是1200m².

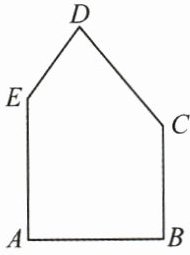
13. (10 分)(2025·无锡模拟)有一块形状如图的五边形余料 $ ABCDE $,$ AB = AE = 6 $,$ BC = 5 $,$ \angle A = \angle B = 90° $,$ \angle C = 135° $,$ \angle E ＞ 90° $,要在这块余料中截取一块矩形材料,其中一条边在 $ AE $ 上,并使所截矩形材料的面积尽可能大。
(1)若所截矩形材料的一条边是 $ BC $ 或 $ AE $,求矩形材料的面积。
(2)能否截出比(1)中面积更大的矩形材料？如果能,求出该矩形材料面积的最大值；如果不能,请说明理由。

答案： 解：
(1)①若所截矩形材料的一条边是BC，如图
(1)，过点C作CF⊥AE于点F.
∵∠A=∠B=90°，
∴四边形ABCF为矩形.
∵AB=AE=6，BC=5，
∴S₁=AB·BC=6×5=30.
②若所截矩形材料的一条边是AE，如图
(2)，过点E作EF//AB交CD于点F，过点F作FG⊥AB于点G，过点C作CH⊥FG于点H，则四边形AEFG为矩形，四边形BCHG为矩形.
∵∠DCB=135°，
∴∠FCH=45°.
∴△CHF为等腰直角三角形.
∴FG=AE=6，HG=BC=5，BG=CH=FH=FG-HG=6-5=1.
∴AG=AB-BG=6-1=5.
∴S₂=AE·AG=6×5=30.
综上所述，矩形材料的面积为30.
(2)能.如图
(3)，在CD上取点F，过点F作FM⊥AB于点M，FN⊥AE于点N，过点C作CG⊥FM于点G，则四边形ANFM为矩形，四边形BCGM为矩形.
∴MG=BC=5，BM=CG.
∵∠DCB=135°，
∴∠FCG=45°.
∴△CGF为等腰直角三角形.
∴FG=CG.
设AM=x，则BM=6-x.
∴FM=GM+FG =GM+CG =BC+BM =11-x.
∴S=AM·FM =x(11-x)=-x²+11x =-(x-5.5)²+30.25.
∴当x=5.5时，S的最大值为30.25.