第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
7. (3 分)(2025·杭州拱墅区期末)二次函数 $ y = ax^2 + ax + c^2 + 1 $($ a $,$ c $ 为常数,且 $ a \neq 0 $)的图象可能是 (

A
)
答案:
A
8. (3 分)(2025·西安模拟)函数 $ y = ax + b $ 和 $ y = ax^2 + bx + c $ 在同一直角坐标系内的图象大致是 (

D
)
答案:
D
9. (3 分)已知点 $ A(5, y_1) $ 和 $ B(n, y_2) $ 在二次函数 $ y = x^2 - 2x + m $ 的图象上.若 $ y_1 > y_2 $,则符合条件的整数 $ n $ 的个数为
7
.
答案:
7 解析:$\because y=x^{2}-2x+m$,$\therefore$抛物线开口向上,对称轴为直线$x=1$.$\therefore$点$A(5,y_{1})$关于直线$x=1$的对称点为$(-3,y_{1})$,当$x>1$时,$y$随$x$的增大而增大,当$x<1$时,$y$随$x$的增大而减小.$\because$点$A(5,y_{1})$,$B(n,y_{2})$在二次函数$y=x^{2}-2x+m$的图象上,且$y_{1}>y_{2}$,$\therefore -3<n<5$.$\therefore n$的值为$-2,-1,0,1,2,3,4$.$\therefore$符合条件的整数$n$的个数为7.
10. (3 分)(2025·杭州市滨江区期末)在平面直角坐标系中,设函数 $ y = ax^2 + (a - 1)x - 1 $($ a $ 是常数,$ a \neq 0 $).
①无论 $ a $ 取何值,该函数图象必定经过两个定点;
②若在 $ -1 < x < 0 $ 时,始终有 $ y $ 随 $ x $ 的增大而减小,则 $ -1 \leq a \leq 1 $ 且 $ a \neq 0 $.
以上结论正确的是
①无论 $ a $ 取何值,该函数图象必定经过两个定点;
②若在 $ -1 < x < 0 $ 时,始终有 $ y $ 随 $ x $ 的增大而减小,则 $ -1 \leq a \leq 1 $ 且 $ a \neq 0 $.
以上结论正确的是
①②
.(填序号)
答案:
①② 解析:①$y=ax^{2}+(a-1)x-1=ax(x+1)-(x+1)=(x+1)(ax-1)$,当$x=-1$时,$y=0$;当$x=0$时,$y=-1$.$\therefore$无论$a$取何值,该函数图象必过两定点$(-1,0)$,$(0,-1)$,故①正确.②函数$y=ax^{2}+(a-1)x-1$($a$是常数,$a≠0$)的对称轴为直线$x=-\frac{a-1}{2a}=-\frac{1}{2}+\frac{1}{2a}$.当$a>0$时,如果在$-1<x<0$时,始终有$y$随$x$的增大而减小,则$-\frac{1}{2}+\frac{1}{2a}\geqslant0$,解得$a\leqslant1$.$\therefore 0<a\leqslant1$.当$a<0$时,如果在$-1<x<0$时,始终有$y$随$x$的增大而减小,则$-\frac{1}{2}+\frac{1}{2a}\leqslant-1$,解得$a\geqslant-1$.$\therefore -1\leqslant a<0$.综上所述,若在$-1<x<0$时,始终有$y$随$x$的增大而减小,则$-1\leqslant a\leqslant1$且$a≠0$,故②正确.
11. (10 分)(2025·济南历下区模拟)如图,已知抛物线 $ y = -x^2 + mx + 3 $ 与 $ x $ 轴交于 $ A $,$ B $ 两点,与 $ y $ 轴交于点 $ C $,点 $ B $ 的坐标为$(3, 0)$.
(1)求 $ m $ 的值及抛物线的顶点坐标;
(2)$ P $ 是抛物线对称轴 $ l $ 上的一个动点,当 $ PA + PC $ 的值最小时,求点 $ P $ 的坐标.
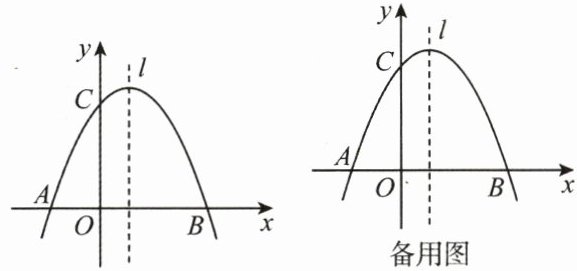
(1)求 $ m $ 的值及抛物线的顶点坐标;
(2)$ P $ 是抛物线对称轴 $ l $ 上的一个动点,当 $ PA + PC $ 的值最小时,求点 $ P $ 的坐标.

答案:
(1)把点$B(3,0)$代入解析式,得$0=-3^{2}+3m+3$,解得$m=2$.$\therefore$抛物线的函数解析式为$y=-x^{2}+2x+3$.顶点坐标的横坐标为$-\frac{b}{2a}=1$.把$x=1$代入解析式,得$y=4$,$\therefore$抛物线的顶点坐标为$(1,4)$.
(2)$\because$点$A$,$B$关于抛物线的对称轴对称,$\therefore PA=PB$.$\therefore$如图,连接$BC$交抛物线的对称轴于点$P$,则此时$PA+PC$的值最小. 将$x=0$代入$y=-x^{2}+2x+3$中,得$y=3$,$\therefore$点$C$的坐标为$(0,3)$.设直线$BC$的解析式为$y=kx+b$.$\therefore \begin{cases} 0=3k+b, \\ 3=b, \end{cases}$解得$\begin{cases} k=-1, \\ b=3. \end{cases}$$\therefore$直线$BC$的函数解析式为$y=-x+3$.将$x=1$代入,得$y=2$,$\therefore$点$P$的坐标为$(1,2)$.
将$x=0$代入$y=-x^{2}+2x+3$中,得$y=3$,$\therefore$点$C$的坐标为$(0,3)$.设直线$BC$的解析式为$y=kx+b$.$\therefore \begin{cases} 0=3k+b, \\ 3=b, \end{cases}$解得$\begin{cases} k=-1, \\ b=3. \end{cases}$$\therefore$直线$BC$的函数解析式为$y=-x+3$.将$x=1$代入,得$y=2$,$\therefore$点$P$的坐标为$(1,2)$.
(1)把点$B(3,0)$代入解析式,得$0=-3^{2}+3m+3$,解得$m=2$.$\therefore$抛物线的函数解析式为$y=-x^{2}+2x+3$.顶点坐标的横坐标为$-\frac{b}{2a}=1$.把$x=1$代入解析式,得$y=4$,$\therefore$抛物线的顶点坐标为$(1,4)$.
(2)$\because$点$A$,$B$关于抛物线的对称轴对称,$\therefore PA=PB$.$\therefore$如图,连接$BC$交抛物线的对称轴于点$P$,则此时$PA+PC$的值最小.
 将$x=0$代入$y=-x^{2}+2x+3$中,得$y=3$,$\therefore$点$C$的坐标为$(0,3)$.设直线$BC$的解析式为$y=kx+b$.$\therefore \begin{cases} 0=3k+b, \\ 3=b, \end{cases}$解得$\begin{cases} k=-1, \\ b=3. \end{cases}$$\therefore$直线$BC$的函数解析式为$y=-x+3$.将$x=1$代入,得$y=2$,$\therefore$点$P$的坐标为$(1,2)$.
将$x=0$代入$y=-x^{2}+2x+3$中,得$y=3$,$\therefore$点$C$的坐标为$(0,3)$.设直线$BC$的解析式为$y=kx+b$.$\therefore \begin{cases} 0=3k+b, \\ 3=b, \end{cases}$解得$\begin{cases} k=-1, \\ b=3. \end{cases}$$\therefore$直线$BC$的函数解析式为$y=-x+3$.将$x=1$代入,得$y=2$,$\therefore$点$P$的坐标为$(1,2)$. 12. (12 分)如果二次函数的二次项系数为 $ 1 $,则此二次函数可表示为 $ y = x^2 + px + q $,我们称$[p, q]$为此函数的“特征数”,如二次函数 $ y = x^2 + 2x + 3 $ 的特征数为$[2, 3]$.
(1)若一个函数的特征数为$[-2, 1]$,则该函数图象的顶点坐标为 ____
(2)探究以下问题:
①若一个函数的特征数为$[4, -1]$,将此函数的图象先向右平移 $ 1 $ 个单位长度,再向上平移 $ 1 $ 个单位长度,求得到的图象对应函数的特征数;
②若一个函数的特征数为$[2, 3]$,将此函数的图象经过怎样的平移才能使得到的图象对应函数的特征数为$[3, 4]$?
(1)若一个函数的特征数为$[-2, 1]$,则该函数图象的顶点坐标为 ____
(1,0)
.(2)探究以下问题:
①若一个函数的特征数为$[4, -1]$,将此函数的图象先向右平移 $ 1 $ 个单位长度,再向上平移 $ 1 $ 个单位长度,求得到的图象对应函数的特征数;
②若一个函数的特征数为$[2, 3]$,将此函数的图象经过怎样的平移才能使得到的图象对应函数的特征数为$[3, 4]$?
(2)①由题意可得$y=x^{2}+4x-1=(x+2)^{2}-5$,$\therefore$将此函数的图象先向右平移1个单位长度,再向上平移1个单位长度后得$y=(x+2-1)^{2}-5+1=(x+1)^{2}-4=x^{2}+2x-3$.$\therefore$图象对应的函数的特征数为$[2,-3]$.②$\because$一个函数的特征数为$[2,3]$,$\therefore$函数解析式为$y=x^{2}+2x+3=(x+1)^{2}+2$.$\because$一个函数的特征数为$[3,4]$,$\therefore$函数解析式为$y=x^{2}+3x+4=\left(x+\frac{3}{2}\right)^{2}+\frac{7}{4}$.$\therefore$可将原函数的图象向左平移$\frac{1}{2}$个单位长度,再向下平移$\frac{1}{4}$个单位长度得到.
答案:
(1)$(1,0)$
(2)①由题意可得$y=x^{2}+4x-1=(x+2)^{2}-5$,$\therefore$将此函数的图象先向右平移1个单位长度,再向上平移1个单位长度后得$y=(x+2-1)^{2}-5+1=(x+1)^{2}-4=x^{2}+2x-3$.$\therefore$图象对应的函数的特征数为$[2,-3]$.②$\because$一个函数的特征数为$[2,3]$,$\therefore$函数解析式为$y=x^{2}+2x+3=(x+1)^{2}+2$.$\because$一个函数的特征数为$[3,4]$,$\therefore$函数解析式为$y=x^{2}+3x+4=\left(x+\frac{3}{2}\right)^{2}+\frac{7}{4}$.$\therefore$可将原函数的图象向左平移$\frac{1}{2}$个单位长度,再向下平移$\frac{1}{4}$个单位长度得到.
(1)$(1,0)$
(2)①由题意可得$y=x^{2}+4x-1=(x+2)^{2}-5$,$\therefore$将此函数的图象先向右平移1个单位长度,再向上平移1个单位长度后得$y=(x+2-1)^{2}-5+1=(x+1)^{2}-4=x^{2}+2x-3$.$\therefore$图象对应的函数的特征数为$[2,-3]$.②$\because$一个函数的特征数为$[2,3]$,$\therefore$函数解析式为$y=x^{2}+2x+3=(x+1)^{2}+2$.$\because$一个函数的特征数为$[3,4]$,$\therefore$函数解析式为$y=x^{2}+3x+4=\left(x+\frac{3}{2}\right)^{2}+\frac{7}{4}$.$\therefore$可将原函数的图象向左平移$\frac{1}{2}$个单位长度,再向下平移$\frac{1}{4}$个单位长度得到.
查看更多完整答案,请扫码查看


