《2025年初中同步练习册分层卷九年级数学上册人教版》

6. (11分)如图,将 $ \triangle ABC $绕点 $ A $逆时针旋转得到 $ \triangle ADE $,点 $ C $和点 $ E $是对应点,若 $ \angle CAE = 90° $,$ AB = 1 $,求 $ BD $的长。

答案： 解：
∵将△ABC绕点A逆时针旋转得到△ADE，点C和点E是对应点，
∴AB=AD=1，∠BAD=∠CAE=90°.
∴BD=√(AB²+AD²)=√2.
∴BD的长为√2.

7. (3分)(2025·遵义期中)如图,$ P $是等边三角形 $ ABC $内一点,且 $ PA = 6 $,$ PB = 8 $,$ PC = 10 $,若将 $ \triangle PAC $绕点 $ A $逆时针旋转后得到 $ \triangle P'AB $。给出下列四个结论：① $ PP' = 6 $； ② $ AP^2 + BP^2 = CP^2 $； ③ $ \angle APB = 150° $； ④ $ S_{\triangle BPP'} = 24 $。其中,正确的结论有 (D)

A.1个
B.2个
C.3个
D.4个

答案： D

8. (3分)(2025·泰州期末)如图,四边形 $ ABCD $为正方形,$ \triangle AEF $为等边三角形,将 $ \triangle AEF $绕点 $ A $旋转,若 $ BE = DF $,则 $ \angle BAE $的度数为 (D)

A.$ 15° $
B.$ 30° $
C.$ 15° $或 $ 105° $
D.$ 15° $或 $ 165° $

答案： D 解析：分两种情况：当△AEF绕点A旋转到正方形ABCD的内部时，如图所示
∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°.
∵△AEF是等边三角形，
∴AE=AF，∠EAF=60°.
∵BE=DF，
∴△ABE≌△ADF(SSS).
∴∠BAE=∠DAF=1/2(∠BAD - ∠EAF)=15°.当△AEF绕点A旋转到正方形ABCD的外部时，如图所示.
∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°.
∵△AEF是等边三角形，
∴AE=AF，∠EAF=60°.
∵BE=DF，
∴△ABE≌△ADF(SSS).
∴∠BAE=∠DAF=1/2(360° - ∠BAD + ∠EAF)=165°.综上所述，∠BAE的度数为15°或165°.

9. (3分)(2025·南昌红谷滩区期中)如图,在四边形 $ ABCD $中,$ \angle DAB = \angle CBA = 90° $,将 $ CD $绕点 $ D $逆时针旋转 $ 90° $至 $ DE $,连接 $ AE $,若 $ AD = 6 $,$ BC = 10 $,则 $ \triangle ADE $的面积是 ______ 。

12

答案： 12 解析：如图，过点D作DH⊥BC，过点E作EF⊥AD交AD的延长线于点F，则四边形ABHD为矩形，
∴AD//BC，HC=BC - BH=BC - AD=10 - 6=4.
∵将CD绕点D逆时针旋转90°至DE，
∴CD=DE，∠CDF+∠EDF=90°.
∵∠DEF+∠EDF=90°，
∴∠CDF=∠DEF.
∵AD//BC，
∴∠CDF=∠BCD.
∴∠BCD=∠DEF.
∵DH⊥BC，EF⊥AD，
∴∠EFA=∠DHC=90°.
∴△DHC≌△DFE(AAS).
∴EF=HC=4.
∴S△ADE=1/2AD·EF=1/2×6×4=12.

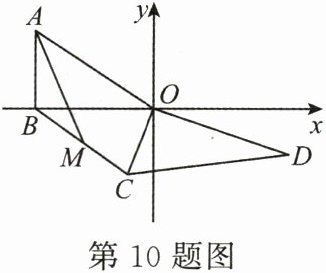
10. (3分)(2025·泰安质检)如图,在平面直角坐标系中,$ Rt \triangle AOB $的一条直角边 $ OB $在 $ x $轴上,点 $ A 的坐标为 (-6,4) $；在 $ Rt \triangle COD $中,$ \angle COD = 90° $,$ OD = 4\sqrt{3} $,$ \angle D = 30° $,连接 $ BC $,$ M $是 $ BC $中点,连接 $ AM $。将 $ Rt \triangle COD $以点 $ O $为旋转中心按顺时针方向旋转,在旋转过程中,线段 $ AM $的最小值是 3。

答案： 3

11. (18分)(2025·天津滨海新区期中)如图,一张长为 $ 8 cm $、宽为 $ 4 cm $的矩形纸片 $ ABCD $。
(1)如图(1),将矩形纸片 $ ABCD $沿着对角线 $ AC $剪开,将 $ \triangle ABC $绕点 $ A $逆时针旋转得到 $ \triangle AEF $,使边 $ AD $和 $ AE $在同一直线上。连接 $ CF $,请写出 $ \triangle ACF $的形状,并说明理由；
(2)如图(2),将(1)中的 $ \triangle AEF $绕点 $ A $顺时针旋转(转动的度数小于 $ 45° $),边 $ AE $与边 $ DC $相交于点 $ M $。当旋转度数为 $ 30° $时,求点 $ E $到 $ CD $的距离。

答案： 解：
(1)△ACF是等腰直角三角形.理由如下：
∵四边形ABCD是矩形，
∴∠BAD=90°.
∵将△ABC绕点A逆时针旋转得到△AEF，边AD和AE在同一直线上，
∴AF=AC，∠EAF=∠BAC.
∴∠CAF=∠CAE+∠EAF=∠CAE+∠BAC=∠BAD=90°.
∴△ACF是等腰直角三角形.
(2)如图，作EH⊥DC于点H，交AB于点G.
∵AB=CD=8 cm，AD=4 cm，
∴AE=AB=8 cm.
∵∠DAG=∠ADH=∠DHG=90°，
∴四边形AGHD是矩形.
∴GH=AD=4 cm，∠AGE=90°，GE//AD.
∵将△AEF绕点A顺时针旋转，旋转度数为30°，
∴∠AEG=∠DAE=30°.
∴AG=1/2AE=4 cm.
∴GE=√(AE² - AG²)=√(8² - 4²)=4√3(cm).
∴EH=GE - GH=(4√3 - 4)cm.
∴点E到CD的距离为(4√3 - 4)cm.