第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
10. (3分)(2025·新乡期末)下面关于$x$的方程中:①$ax^{2}+x + 2 = 0$;②$3(x - 9)^{2}-(x + 1)^{2}= 1$;③$x + 3= \frac{1}{x}$;④$x^{2}-a = 0$($a$为任意实数);⑤$\sqrt{x + 1}= x - 1$.一元二次方程有 (
A.1个
B.2个
C.3个
D.4个
B
)A.1个
B.2个
C.3个
D.4个
答案:
B
11. (3分)已知关于$x的一元二次方程(a - 1)x^{2}-2x + a^{2}-1 = 0有一个根为x = 0$,则$a$的值为 (
A.$0$
B.$\pm 1$
C.$1$
D.$-1$
D
)A.$0$
B.$\pm 1$
C.$1$
D.$-1$
答案:
D
12. (3分)扬帆中学有一块长$30m$、宽$20m$的矩形空地,计划在这块空地上划出四分之一的区域(图中阴影部分)种花,小禹同学设计的方案如图所示,求花带的宽度.设花带的宽度为$x m$,则可列方程为 (
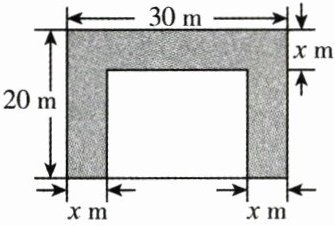
A.$(30 - x)(20 - x)= \frac{3}{4}×20×30$
B.$(30 - 2x)(20 - x)= \frac{1}{4}×20×30$
C.$30x + 2×20x= \frac{1}{4}×20×30$
D.$(30 - 2x)(20 - x)= \frac{3}{4}×20×30$
D
)
A.$(30 - x)(20 - x)= \frac{3}{4}×20×30$
B.$(30 - 2x)(20 - x)= \frac{1}{4}×20×30$
C.$30x + 2×20x= \frac{1}{4}×20×30$
D.$(30 - 2x)(20 - x)= \frac{3}{4}×20×30$
答案:
D
13. (3分)(2025·包头质检)关于$x的一元二次方程(m - 3)x^{2}+m^{2}x = 9x + 5化为一般形式后不含x$的一次项,则$m$的值为
-3
.
答案:
-3
14. (3分)(2025·青岛期中)生物兴趣小组的同学将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件,若全组有$x$名同学,则根据题意列出的方程是
x²-x-182=0
.(化为一般形式)
答案:
x²-x-182=0
15. (6分)已知关于$x的方程(m^{2}-9)x^{2}+(m + 3)x - 5 = 0$.
(1)当$m$为何值时,此方程是一元一次方程?并求出此时方程的解.
(2)当$m$为何值时,此方程是一元二次方程?并写出这个方程的二次项系数、一次项系数及常数项.
(1)当$m$为何值时,此方程是一元一次方程?并求出此时方程的解.
(2)当$m$为何值时,此方程是一元二次方程?并写出这个方程的二次项系数、一次项系数及常数项.
答案:
解:
(1)根据一元一次方程的定义可知m²-9=0,m+3≠0,解得m=3.此时方程为6x-5=0,解得x=$\frac{5}{6}$.
(2)根据一元二次方程的定义可知m²-9≠0,解得m≠±3.该方程的二次项系数为m²-9(m≠±3),一次项系数为m+3,常数项为-5.
(1)根据一元一次方程的定义可知m²-9=0,m+3≠0,解得m=3.此时方程为6x-5=0,解得x=$\frac{5}{6}$.
(2)根据一元二次方程的定义可知m²-9≠0,解得m≠±3.该方程的二次项系数为m²-9(m≠±3),一次项系数为m+3,常数项为-5.
16. (6分)(2025·淮南八公山区质检)定义:如果一元二次方程$ax^{2}+bx + c = 0(a \neq 0)满足a - b + c = 0$,那么我们称这个方程为“和谐方程”.
(1)判断一元二次方程$2x^{2}+7x + 5 = 0$是否为“和谐方程”,并说明理由;
(2)已知$3x^{2}-mx + n = 0是关于x$的“和谐方程”,若$x = -2$是此“和谐方程”的一个根,求$m$,$n$的值.
(1)判断一元二次方程$2x^{2}+7x + 5 = 0$是否为“和谐方程”,并说明理由;
(2)已知$3x^{2}-mx + n = 0是关于x$的“和谐方程”,若$x = -2$是此“和谐方程”的一个根,求$m$,$n$的值.
答案:
解:
(1)一元二次方程2x²+7x+5=0是“和谐方程”.理由如下:在一元二次方程2x²+7x+5=0中,a=2,b=7,c=5.
∵2-7+5=0,
∴一元二次方程2x²+7x+5=0是“和谐方程”.
(2)
∵3x²-mx+n=0是关于x的“和谐方程”,
∴3-(-m)+n=0,即3+m+n=0.
∵x=-2是此“和谐方程”的一个根,
∴3×(-2)²-m×(-2)+n=0,即$\begin{cases}3+m+n=0,\\12+2m+n=0,\end{cases}$解得$\begin{cases}m=-9,\\n=6.\end{cases}$
∴m的值为-9,n的值为6.
(1)一元二次方程2x²+7x+5=0是“和谐方程”.理由如下:在一元二次方程2x²+7x+5=0中,a=2,b=7,c=5.
∵2-7+5=0,
∴一元二次方程2x²+7x+5=0是“和谐方程”.
(2)
∵3x²-mx+n=0是关于x的“和谐方程”,
∴3-(-m)+n=0,即3+m+n=0.
∵x=-2是此“和谐方程”的一个根,
∴3×(-2)²-m×(-2)+n=0,即$\begin{cases}3+m+n=0,\\12+2m+n=0,\end{cases}$解得$\begin{cases}m=-9,\\n=6.\end{cases}$
∴m的值为-9,n的值为6.
查看更多完整答案,请扫码查看


