《2025年初中同步练习册分层卷九年级数学上册人教版》

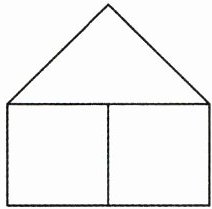
8. (3 分)(2025·马鞍山质检)用总长 10 m 的铝合金材料做一个如图所示的窗框(不计损耗),窗框的上部是等腰直角三角形,下部是两个全等的矩形,窗框的总面积为$ 3 m^2($材料的厚度忽略不计). 若设等腰直角三角形的斜边长为 x m,下列方程符合题意的是 (D)

A.$ (2 - \sqrt{2})x + 3(\frac{3}{x} - \frac{x}{4}) = 10 $
B.$ (2 + \sqrt{2})x + 3(\frac{3}{x} + \frac{x}{4}) = 10 $
C.$ x \cdot \frac{10 - 2x - \sqrt{2}x}{3} + \frac{1}{2}x^2 = 3 $
D.$ x \cdot \frac{10 - 2x - \sqrt{2}x}{3} + \frac{1}{4}x^2 = 3 $

答案： D 解析：设等腰直角三角形的斜边长为x m，
则等腰直角三角形的直角边长为$\frac{\sqrt{2}}{2}x$ m，下部两个全等矩形合成的大矩形的长为x m，宽为$\frac{10-2x-\sqrt{2}x}{3}$ m.
依题意，得$x\cdot\frac{10-2x-\sqrt{2}x}{3}+\frac{1}{2}(\frac{\sqrt{2}}{2}x)^{2}=3$，
即$x\cdot\frac{10-2x-\sqrt{2}x}{3}+\frac{1}{4}x^{2}=3$.

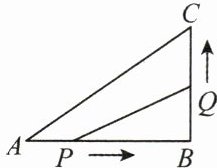
9. (14 分)(2025·深圳福田区质检)如图,在 $ \triangle ABC $ 中, $ \angle ABC = 90° $, $ AB = 4 cm $, $ BC = 3 cm $,动点 P,Q 分别从点 A,B 同时开始移动(移动方向如图所示),点 P 的速度为 $ \frac{1}{2} cm/s $,点 Q 的速度为 1 cm/s,点 Q 移动到点 C 后停止,点 P 也随之停止移动,若使 $ \triangle PBQ $ 的面积为 $ \frac{15}{4} cm^2 $,则点 P,Q 运动的时间是多少秒?

答案： 解：设动点P，Q运动t(t≤3)s时，能使△PBQ的面积为$\frac{15}{4}\ cm^{2}$，则BP的长为$(4-\frac{1}{2}t)\ cm$，BQ的长为t cm.
根据题意，得$\frac{1}{2}(4-\frac{1}{2}t)× t=\frac{15}{4}$，
解得t₁=3，t₂=5(舍去).
答：动点P，Q运动3 s时，能使△PBQ的面积为$\frac{15}{4}\ cm^{2}$.

10. (16 分)(2025·廊坊固安县期中)已知一块矩形铁皮长 60 cm、宽 24 cm.
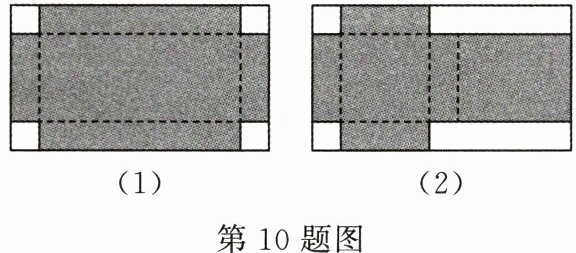
(1)如图(1),在铁皮的四角各切去一个同样的正方形,然后沿虚线折起,制作成一个底面积为$ 832 cm^2 $的无盖盒子.设切去的正方形的边长为 x cm,根据题意可列方程为(60-2x)(24-2x)=832.
(2)现要制作一个有盖的长方体盒子,为了合理使用材料,嘉琪设计了如图(2)的裁剪方案,空白部分为裁剪下来的边角料,其中左侧两个空白部分为正方形,能否折出底面积为$ 486 cm^2 $的有盖盒子(盒盖与盒底的大小、形状完全相同)? 如果能,请求出盒子的体积；如果不能,请说明理由.

答案：
(1)(60-2x)(24-2x)=832
(2)能.设切去的正方形的边长为y cm，则折成的长方体盒子的底面为长$(\frac{60}{2}-y)\ cm$、宽(24-2y)cm的矩形.
依题意，得$(\frac{60}{2}-y)(24-2y)=486$，
解得y₁=3，y₂=39(不符合题意，舍去).
∴盒子的体积为486×3=1458(cm³).
答：能折出底面积为486 cm²的有盖盒子，盒子的体积为1458 cm³.