《2025年初中同步练习册分层卷九年级数学上册人教版》

4. (3分)(2025·台州期中)某市中心广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为 $ 3 $ m,此时距喷水管的水平距离为 $ \frac{1}{2} $ m,在如图所示的直角坐标系中,这个喷泉的函数解析式是 (C)

A.$ y = -\left(x - \frac{1}{2}\right)^2 + 3 $
B.$ y = -3\left(x + \frac{1}{2}\right)^2 + 3 $
C.$ y = -12\left(x - \frac{1}{2}\right)^2 + 3 $
D.$ y = -12\left(x + \frac{1}{2}\right)^2 + 3 $

答案： C

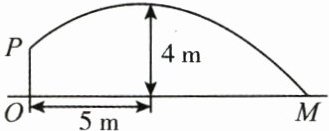
5. (3分)(2024·广西中考)如图,壮壮同学投掷实心球,出手点 $ P $ 处的高度 $ OP $ 是 $ \frac{7}{4} $ m,出手后实心球沿一段抛物线运行,到达最高点时,水平距离是 $ 5 $ m,高度是 $ 4 $ m.若实心球落地点为 $ M $,则 $ OM = $$\frac{35}{3}$m.

答案： $\frac{35}{3}$

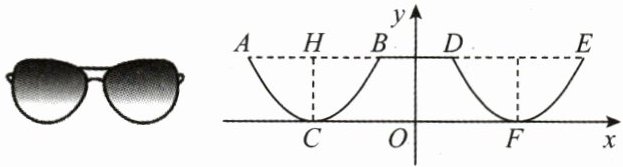
6. (3分)(2025·广州太和县期中)为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于 $ y $ 轴对称, $ AE // x $ 轴, $ AB = 4 $ cm,最低点 $ C $ 在 $ x $ 轴上,高 $ CH = 1 $ cm, $ BD = 2 $ cm,则右轮廓 $ DFE $ 所在抛物线的函数解析式为 (B)

A.$ y = \frac{1}{2}(x - 3)^2 $
B.$ y = \frac{1}{4}(x - 3)^2 $
C.$ y = -\frac{1}{2}(x - 3)^2 $
D.$ y = -\frac{1}{4}(x - 3)^2 $

答案： B

7. (3分)(2025·沧州期末)如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的,正常水位时,大孔水面宽度为 $ 20 $ m,顶点距水面 $ 6 $ m,小孔顶点距水面 $ 4.5 $ m,当水位上涨刚好淹没小孔时,大孔的水面宽度为 (C)

A.$ 5 $ m
B.$ 5\sqrt{3} $ m
C.$ 10 $ m
D.$ 10\sqrt{3} $ m

答案： C

8. (3分)(2025·苏州质检)图(1)是一个瓷碗,图(2)是其截面图,碗体 $ DEC $ 呈抛物线状(碗体厚度不计),碗口宽 $ CD = 12 $ cm,此时面汤最大深度 $ EG = 8 $ cm.如图(3),把瓷碗绕点 $ B $ 缓缓倾斜倒出部分面汤,当 $ \angle ABM = 45° $ 时停止,此时碗中液面宽度 $ CH = $$\frac{15\sqrt{2}}{2}$cm.

答案： $\frac{15\sqrt{2}}{2}$