第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
10. (3 分)(2025·保定模拟)如图,在平面直角坐标系中,$\odot P与x轴分别交于A$,$B$两点,点$P的坐标为(3,-1)$,$AB = 2\sqrt{3}$.将$\odot P沿着与y$轴平行的方向平移
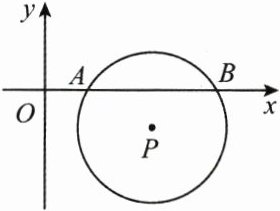
A.1
B.2
C.3
D.1 或 3
2或0
个单位长度时,$\odot P与x$轴相切. (D
)
A.1
B.2
C.3
D.1 或 3
答案:
D
11. (3 分)已知$\odot O的半径为r$,点$O到直线l的距离为d$,且$|d - 3|+(5 - 2r)^{2}= 0$,则直线$l与\odot O$的位置关系是
相离
.
答案:
相离
12. (3 分)(2025·宁波慈溪市模拟)如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,$AC = 2$,以点$C$为圆心、$r$为半径作圆.若该圆与线段$AB$只有一个交点,则$r$的取值范围为

$r=\sqrt{3}$或$2<r≤2\sqrt{3}$
.
答案:
$r=\sqrt{3}$或$2<r≤2\sqrt{3}$
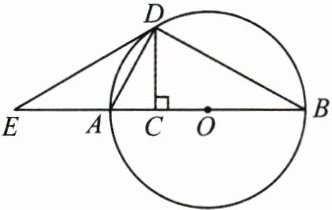
13. (8 分)如图,$AB为\odot O$的直径,取$OA的中点C$,过点$C作CD\perp AB交\odot O于点D$,点$D在AB$的上方,连接$AD$,$BD$,点$E在线段CA$的延长线上,且$\angle ADE = \angle ABD$.求:
(1)$\angle ABD$的度数;
(2)直线$DE与\odot O$的公共点个数.
(1)$\angle ABD$的度数;
(2)直线$DE与\odot O$的公共点个数.

答案:
解:
(1)如图,连接 OD,则 OA = OD。
∵C 为 OA 的中点,CD⊥AB,
∴AD = OD。
∴OA = OD = AD。
∴△OAD 是等边三角形。
∴∠AOD = 60°。
∴∠ABD = 30°。

(2)
∵∠ADE = ∠ABD,
∴∠ADE = 30°。
∵∠ADO = 60°,
∴∠ODE = 90°。
∴OD⊥DE。
∴DE 是$\odot O$的切线。
∴直线 DE 与$\odot O$的公共点个数为 1。
解:
(1)如图,连接 OD,则 OA = OD。
∵C 为 OA 的中点,CD⊥AB,
∴AD = OD。
∴OA = OD = AD。
∴△OAD 是等边三角形。
∴∠AOD = 60°。
∴∠ABD = 30°。

(2)
∵∠ADE = ∠ABD,
∴∠ADE = 30°。
∵∠ADO = 60°,
∴∠ODE = 90°。
∴OD⊥DE。
∴DE 是$\odot O$的切线。
∴直线 DE 与$\odot O$的公共点个数为 1。
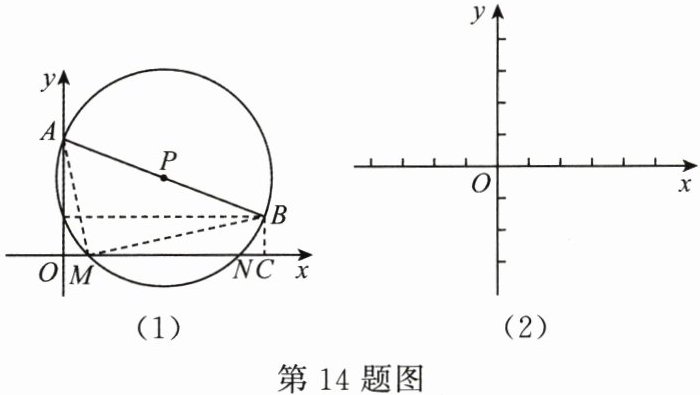
14. (10 分)某数学家给出了一元二次方程$x^{2}+bx + c = 0$的几何解法:如图(1),在平面直角坐标系中,已知点$A(0,1)$,$B(-b,c)$,以$AB为直径作\odot P$.若$\odot P交x轴于点M(m,0)$,$N(n,0)$,则$m$,$n为方程x^{2}+bx + c = 0$的两个实数根.
[探究](1)由勾股定理,得$AM^{2}= 1^{2}+m^{2}$,$BM^{2}= c^{2}+(-b - m)^{2}$,$AB^{2}= (1 - c)^{2}+b^{2}$.在$Rt\triangle ABM$中,$AM^{2}+BM^{2}= AB^{2}$,所以$1^{2}+m^{2}+c^{2}+(-b - m)^{2}= (1 - c)^{2}+b^{2}$.
化简,得$m^{2}+bm + c = 0$.
同理可得______.
所以$m$,$n为方程x^{2}+bx + c = 0$的两个实数根.
[运用](2)在图(2)中的$x轴上画出以方程x^{2}-3x - 2 = 0两根为横坐标的点M$,$N$.
(3)已知点$A(0,1)$,$B(6,9)$,以$AB为直径作\odot C$.判断$\odot C与x$轴的位置关系,并说明理由.
[拓展](4)在平面直角坐标系中,已知两点$A(0,a)$,$B(-b,c)$,若以$AB为直径的圆与x轴有两个交点M$,$N$,则以点$M$,$N$的横坐标为根的一元二次方程是______.
[探究](1)由勾股定理,得$AM^{2}= 1^{2}+m^{2}$,$BM^{2}= c^{2}+(-b - m)^{2}$,$AB^{2}= (1 - c)^{2}+b^{2}$.在$Rt\triangle ABM$中,$AM^{2}+BM^{2}= AB^{2}$,所以$1^{2}+m^{2}+c^{2}+(-b - m)^{2}= (1 - c)^{2}+b^{2}$.
化简,得$m^{2}+bm + c = 0$.
同理可得______.
所以$m$,$n为方程x^{2}+bx + c = 0$的两个实数根.
[运用](2)在图(2)中的$x轴上画出以方程x^{2}-3x - 2 = 0两根为横坐标的点M$,$N$.
(3)已知点$A(0,1)$,$B(6,9)$,以$AB为直径作\odot C$.判断$\odot C与x$轴的位置关系,并说明理由.
[拓展](4)在平面直角坐标系中,已知两点$A(0,a)$,$B(-b,c)$,若以$AB为直径的圆与x轴有两个交点M$,$N$,则以点$M$,$N$的横坐标为根的一元二次方程是______.

答案:
解:
(1)$n^{2}+bn+c=0$
(2)如图,在坐标系中找到 A(0,1),B(3, - 2),连接 AB,分别以点 A,B 为圆心,以大于$\frac{1}{2}AB$的长为半径画弧,连接两弧的交点与 AB 交于点 P,以点 P 为圆心,以 AB 为直径画圆,圆与 x 轴的交点即为点 M,N。

(3)$\odot C$与 x 轴相切。理由如下:
由题意,得$x^{2}-6x + 9 = 0$。
∵△ = $b^{2}-4ac=(-6)^{2}-4×1×9 = 0$,
∴方程$x^{2}-6x + 9 = 0$有两个相等的实数根。
∴$\odot C$与 x 轴只有一个交点,即$\odot C$与 x 轴相切。
(4)$x^{2}+bx + ac = 0$
解:
(1)$n^{2}+bn+c=0$
(2)如图,在坐标系中找到 A(0,1),B(3, - 2),连接 AB,分别以点 A,B 为圆心,以大于$\frac{1}{2}AB$的长为半径画弧,连接两弧的交点与 AB 交于点 P,以点 P 为圆心,以 AB 为直径画圆,圆与 x 轴的交点即为点 M,N。

(3)$\odot C$与 x 轴相切。理由如下:
由题意,得$x^{2}-6x + 9 = 0$。
∵△ = $b^{2}-4ac=(-6)^{2}-4×1×9 = 0$,
∴方程$x^{2}-6x + 9 = 0$有两个相等的实数根。
∴$\odot C$与 x 轴只有一个交点,即$\odot C$与 x 轴相切。
(4)$x^{2}+bx + ac = 0$
查看更多完整答案,请扫码查看


