第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
8. (3分)(2025·太原质检)如图,⊙O是△ABC的内切圆,切点分别为D,E,F,已知AB= BC,∠B= 40°,连接DE,EF,则∠DEF的度数为(
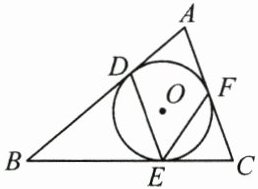
A.40°
B.55°
C.65°
D.70°
B
)
A.40°
B.55°
C.65°
D.70°
答案:
B
9. (3分)(2025·绍兴模拟)如图,等边三角形的边长为a,高为h,内切圆、外接圆的半径分别为r,R,则下列结论不正确的是(
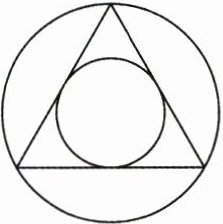
A.h= R+r
B.R= 2r
C.$r= \frac{\sqrt{3}}{4}a$
D.$R= \frac{\sqrt{3}}{3}a$
C
)
A.h= R+r
B.R= 2r
C.$r= \frac{\sqrt{3}}{4}a$
D.$R= \frac{\sqrt{3}}{3}a$
答案:
C
10. (3分)如图,已知C是以AB为直径的半圆O上一点,I是△ABC的内心,AI,BI的延长线分别与半圆O交于点D,E,AB= 6,则DE的长为

3$\sqrt{2}$
.
答案:
3$\sqrt{2}$ 解析:如图,连接OE,OD.
∵I是△ABC的内心,
∴AI,BI分别平分∠CAB,∠ABC.
∴∠CAD=∠BAD,∠ABE=∠CBE.
∴$\widehat{AE}=\widehat{EC}$,$\widehat{CD}=\widehat{BD}$.
∵∠ACB是一个半圆,
∴∠EOD=180°×$\frac{1}{2}$=90°.
∵直径AB=6,
∴OE=OD=3.由勾股定理,得DE=$\sqrt{3^{2}+3^{2}}$=3$\sqrt{2}$.
∵I是△ABC的内心,
∴AI,BI分别平分∠CAB,∠ABC.
∴∠CAD=∠BAD,∠ABE=∠CBE.
∴$\widehat{AE}=\widehat{EC}$,$\widehat{CD}=\widehat{BD}$.
∵∠ACB是一个半圆,
∴∠EOD=180°×$\frac{1}{2}$=90°.
∵直径AB=6,
∴OE=OD=3.由勾股定理,得DE=$\sqrt{3^{2}+3^{2}}$=3$\sqrt{2}$.
11. (3分)(2025·南京鼓楼区期中)如图,⊙O是四边形ABCD的内切圆,若∠BOC= 118°,则∠AOD的度数为
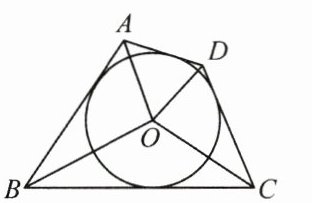
62°
.
答案:
62°
12. (8分)如图,PA,PB与⊙O相切于点A,B,连接AB,PO交⊙O于点C,交AB于点M.求证:点C是△APB的内心.
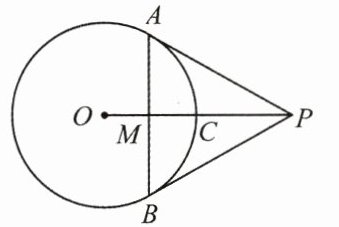

答案:
证明:如图,连接AC,BC,OA,OB.
∵PA,PB与⊙O相切于点A,B,
∴PA=PB,∠APO=∠BPO,OA⊥PA,OB⊥PB.
∵OA=OB,
∴OP垂直平分AB.
∵∠PAC+∠OAC=90°=∠BAC+∠OCA,∠OAC=∠OCA,
∴∠PAC=∠BAC.同理,∠PBC=∠ABC.
∵AC,BC,PC是△APB的角平分线,
∴点C是△APB的内心.
∵PA,PB与⊙O相切于点A,B,
∴PA=PB,∠APO=∠BPO,OA⊥PA,OB⊥PB.
∵OA=OB,
∴OP垂直平分AB.
∵∠PAC+∠OAC=90°=∠BAC+∠OCA,∠OAC=∠OCA,
∴∠PAC=∠BAC.同理,∠PBC=∠ABC.
∵AC,BC,PC是△APB的角平分线,
∴点C是△APB的内心.
13. (9分)(2025·连云港赣榆区期中)一数学研究小组探究了以下相关的两个问题,请你也试试.
(1)如图(1),已知△ABC,BO,CO分别是∠ABC,∠ACB的平分线.试探究∠A与∠BOC的度数之间的关系;
(2)如图(2),已知点O是△ABC内切圆的圆心,点O'是△ABC外接圆的圆心.试探究∠BOC与∠BO'C的度数之间的关系.

(1)如图(1),已知△ABC,BO,CO分别是∠ABC,∠ACB的平分线.试探究∠A与∠BOC的度数之间的关系;
(2)如图(2),已知点O是△ABC内切圆的圆心,点O'是△ABC外接圆的圆心.试探究∠BOC与∠BO'C的度数之间的关系.

答案:
(1)
∵BO,CO分别是∠ABC,∠ACB的平分线,
∴∠1+∠2=$\frac{1}{2}$(180°-∠A).
∴∠BOC=180°-(∠1+∠2)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A.
∴∠BOC=90°+$\frac{1}{2}$∠A.
(2)
∵点O是△ABC内切圆的圆心,
∴BO,CO分别是∠ABC,∠ACB的平分线.由
(1),知∠BOC=90°+$\frac{1}{2}$∠A.
∵点O'是△ABC外接圆的圆心,
∴∠A=$\frac{1}{2}$∠BO'C.
∴∠BOC=90°+$\frac{1}{2}$∠A =90°+$\frac{1}{2}$×$\frac{1}{2}$∠BO'C=90°+$\frac{1}{4}$∠BO'C.
∴∠BOC=90°+$\frac{1}{4}$∠BO'C.
(1)
∵BO,CO分别是∠ABC,∠ACB的平分线,
∴∠1+∠2=$\frac{1}{2}$(180°-∠A).
∴∠BOC=180°-(∠1+∠2)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A.
∴∠BOC=90°+$\frac{1}{2}$∠A.
(2)
∵点O是△ABC内切圆的圆心,
∴BO,CO分别是∠ABC,∠ACB的平分线.由
(1),知∠BOC=90°+$\frac{1}{2}$∠A.
∵点O'是△ABC外接圆的圆心,
∴∠A=$\frac{1}{2}$∠BO'C.
∴∠BOC=90°+$\frac{1}{2}$∠A =90°+$\frac{1}{2}$×$\frac{1}{2}$∠BO'C=90°+$\frac{1}{4}$∠BO'C.
∴∠BOC=90°+$\frac{1}{4}$∠BO'C.
查看更多完整答案,请扫码查看


