《2025年初中同步练习册分层卷九年级数学上册人教版》

1. (3 分)(2025·北京一模)将抛物线 $ y = 5x^2 $ 向右平移 2 个单位长度, 再向下平移 3 个单位长度, 得到的抛物线是 (D)
A.$ y = 5(x + 2)^2 + 3 $
B.$ y = 5(x + 2)^2 - 3 $
C.$ y = 5(x - 2)^2 + 3 $
D.$ y = 5(x - 2)^2 - 3 $

答案： D

2. (3 分)若将抛物线 $ y = (x - 2)^2 - 1 $ 平移得到抛物线 $ y = x^2 $, 则下列平移方法中正确的是 (A)
A.先向左平移 2 个单位长度, 再向上平移 1 个单位长度
B.先向左平移 2 个单位长度, 再向下平移 1 个单位长度
C.先向右平移 2 个单位长度, 再向上平移 1 个单位长度
D.先向右平移 2 个单位长度, 再向下平移 1 个单位长度

答案： A

3. (3 分)(2025·武威期中)将二次函数 $ y = -3(x + 1)^2 $ 的图象先向右平移 2 个单位长度, 再向上平移 4 个单位长度, 所得到的函数解析式为 $y=-3(x-1)^2+4$.

答案： $y=-3(x-1)^2+4$

4. (3 分)(2025·厦门思明区期中)如果保持抛物线 $ y = -4x^2 $ 不动, 把 $ x $ 轴、$ y $ 轴分别向上、向右平移 2 个单位长度, 那么在新坐标系下该抛物线的函数解析式是 $y=-4(x+2)^2-2$.

答案： $y=-4(x+2)^2-2$

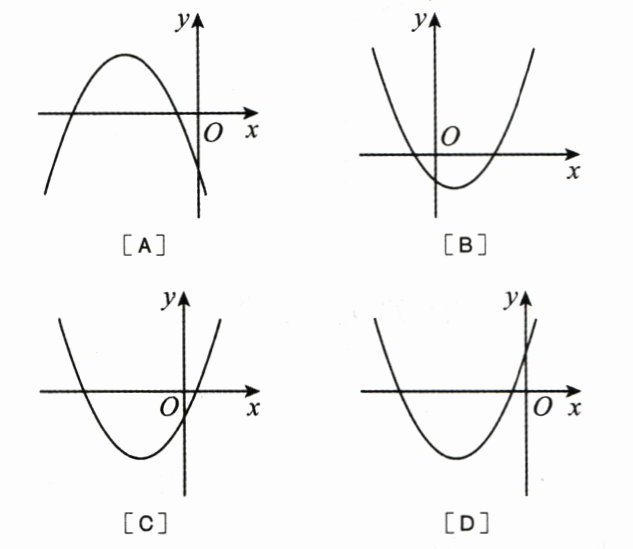
5. (3 分)(2025·广州期中)二次函数 $ y = (x - 1)^2 - 2 $ 的图象可能是 (B)

答案： B

6. (3 分)若 $ A(0, y_1) $, $ B(2, y_2) $, $ C(3, y_3) $ 为二次函数 $ y = (x - 2)^2 + m $ 图象上的三点, 则 $ y_1 $, $ y_2 $, $ y_3 $ 的大小关系为 (D)
A.$ y_1 ＜ y_3 ＜ y_2 $
B.$ y_3 ＜ y_1 ＜ y_2 $
C.$ y_2 ＜ y_1 ＜ y_3 $
D.$ y_2 ＜ y_3 ＜ y_1 $

答案： D

7. (3 分)(2025·温州期中)已知二次函数图象的顶点坐标是 $ (2, -1) $, 形状与抛物线 $ y = 2x^2 $ 相同且开口方向向下, 则这个二次函数的解析式是 $y=-2(x-2)^2-1$.

答案： $y=-2(x-2)^2-1$

8. (9 分)(2025·重庆长寿区质检)已知二次函数 $ y = -(x + 1)^2 + 4 $.
(1)在如图所示的直角坐标系中, 用描点法直接画出该二次函数的图象.(注: 省略作图步骤)
(2)该函数图象的开口向 , 顶点坐标为 , 对称轴为直线 , 函数图象与 $ x $ 轴的交点坐标为 , 与 $ y $ 轴的交点坐标为 .
(3)由图可知, 当 $ -2 \leq x \leq 1 $ 时, 二次函数 $ y = -(x + 1)^2 + 4 $ 的最小值是 , 最大值是 .

答案：
解：
(1)列表如下：

作图如下：

(2)下 (-1，4) $x=-1$ (1，0)和(-3，0) (0，3)
(3)0 4