《2025年初中同步练习册分层卷九年级数学上册人教版》

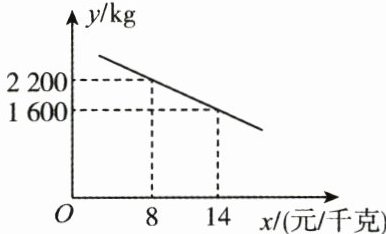
6. (9分)(2023·鞍山中考)网络直播销售已经成为一种热门的销售方式,某果园在网络平台上直播销售荔枝.已知该荔枝的成本为6元/千克,销售价格不高于18元/千克,且每售卖1kg需向网络平台支付2元的相关费用,经过一段时间的直播销售发现,每日销售量$y$(kg)与销售价格$x$(元/千克)之间满足如图所示的一次函数关系.
(1)求$y关于x$的函数解析式；
(2)当每千克荔枝的销售价格定为多少元时,销售这种荔枝日获利最大？最大利润为多少元？

答案：
(1)设一次函数关系为y=kx+b. 由题意，得{8k+b=2200,14k+b=1600, 解得{k=-100,b=3000.
∴y关于x的函数解析式为y=-100x+3000(6≤x≤18).
(2)设每千克荔枝的销售价格定为x元时，销售这种荔枝日获利为w元. 根据题意，得w=(x-6-2)(-100x+3000)=-100x²+3800x-24000=-100(x-19)²+12100.
∵a=-100＜0，对称轴为直线x=19，且销售价格不高于18元/千克，
∴当x=18时，w有最大值为12000.
∴当销售单价定为18元时，销售这种荔枝日获利最大，最大利润为12000元.

7. (3分)(2025·德州陵城区期中)某商场销售的某种商品每件的标价是80元,若按标价的八折销售,仍可盈利24元,市场调查发现：在以标价打八折为销售价的基础上,该种商品每星期可卖出220件,该种商品每降价1元,每星期可多卖20件.设每件商品降价$x$元($x$为整数),每星期的利润为$y$元.以下说法错误的是(D)
[A] 每件商品进价为40元
[B] 降价后每件商品售价为$( 64 - x )$元
[c] 降价后每周可卖$( 220 + 20x )$件
[D] 每星期的利润为$y = ( 84 - x ) ( 220 + 20x )$

答案： D

8. (3分)为了减少空气污染,国家要求限制塑料玩具生产,这样有时企业会被迫停产,经过调研预测,某塑料玩具生产公司一年中每月获得的利润$y$(万元)和月份$n之间满足函数解析式y = - n ^ { 2 } + 14n - 24$,则没有盈利的月份为(D)
[A] 2月和12月
[B] 2月至12月
[C] 1月
[D] 1月、2月和12月

答案： D

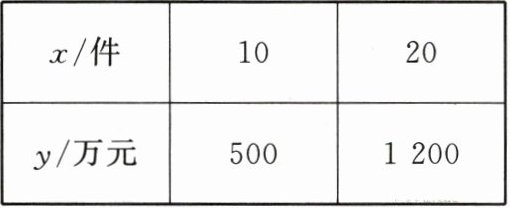
9. (6分)(2025·石家庄期末)某公司分别在A,B两城生产同种产品,共80件,A城生产产品的总成本$y$(万元)由两部分和组成,一部分与$x$(产品数量,单位：件)的平方成正比,比例系数为$a$；另一部分与$x$成正比,比例系数为$b$,生产中得到表中数据.B城生产产品的每件成本为60万元.

(1)$a = $1,$b = $40；
(2)当A城生产10件时,这批产品的总成本的和最少,最小值为4700万元.

答案：
(1)1 40
(2)10 4700