第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. (3 分)(2025·厦门质检)若一个正多边形的中心角等于其内角, 则这个正多边形的边数为 (
A.3
B.4
C.5
D.6
B
)A.3
B.4
C.5
D.6
答案:
B
2. (3 分)如图, 正六边形 $ ABCDEF $ 内接于 $ \odot O $, 连接 $ BD $, 则 $ \angle CBD $ 的度数是 (
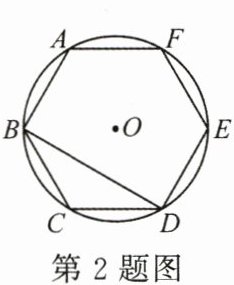
A.$ 30^{\circ} $
B.$ 45^{\circ} $
C.$ 60^{\circ} $
D.$ 90^{\circ} $
A
)
A.$ 30^{\circ} $
B.$ 45^{\circ} $
C.$ 60^{\circ} $
D.$ 90^{\circ} $
答案:
A
3. (3 分)如图, 以 $ AB $ 为边, 在 $ AB $ 的同侧分别作正五边形 $ ABCDE $ 和等边三角形 $ ABF $, 连接 $ FE $, $ FC $, 则 $ \angle EFA $ 的度数是 ____

66°
.
答案:
66°
4. (6 分)(2025·石家庄期末)如图, 已知等边三角形 $ ABC $ 的外接圆 $ \odot O $ 的半径为 $ R $, 求 $ \triangle ABC $ 的边长 $ a $、周长 $ P $、边心距 $ r $ 及面积 $ S $. (用含 $ R $ 的式子表示)


答案:
解:如图,连接 OB,OA,延长 AO 交 BC 于点 D.

∵等边三角形 ABC 的外接圆是⊙O,
∴AD⊥BC,BD=CD= $\frac{1}{2}$BC,∠OBD= $\frac{1}{2}$∠ABC=30°.
∴边心距 r=OD= $\frac{1}{2}$OB= $\frac{1}{2}$R.
由勾股定理,得 BD= $\sqrt{OB^2 - OD^2}$= $\frac{\sqrt{3}}{2}$R,
∴三角形的边长 a=BC=2BD= $\sqrt{3}$R,
AD=AO+OD=R+ $\frac{1}{2}$R= $\frac{3}{2}$R.
∴△ABC 的周长 P=3BC=3× $\sqrt{3}$R=3 $\sqrt{3}$R,
△ABC 的面积 S= $\frac{1}{2}$BC·AD= $\frac{1}{2}$× $\sqrt{3}$R× $\frac{3}{2}$R= $\frac{3\sqrt{3}}{4}$R².
解:如图,连接 OB,OA,延长 AO 交 BC 于点 D.

∵等边三角形 ABC 的外接圆是⊙O,
∴AD⊥BC,BD=CD= $\frac{1}{2}$BC,∠OBD= $\frac{1}{2}$∠ABC=30°.
∴边心距 r=OD= $\frac{1}{2}$OB= $\frac{1}{2}$R.
由勾股定理,得 BD= $\sqrt{OB^2 - OD^2}$= $\frac{\sqrt{3}}{2}$R,
∴三角形的边长 a=BC=2BD= $\sqrt{3}$R,
AD=AO+OD=R+ $\frac{1}{2}$R= $\frac{3}{2}$R.
∴△ABC 的周长 P=3BC=3× $\sqrt{3}$R=3 $\sqrt{3}$R,
△ABC 的面积 S= $\frac{1}{2}$BC·AD= $\frac{1}{2}$× $\sqrt{3}$R× $\frac{3}{2}$R= $\frac{3\sqrt{3}}{4}$R².
5. (6 分)如图, 已知五边形 $ ABCDE $ 是正五边形, 连接 $ AC $, $ AD $. 求证: $ \angle ACD = \angle ADC $.
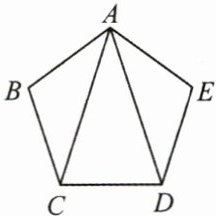

答案:
证明:
∵五边形 ABCDE 为正五边形,
∴AB=AE=BC=ED,∠B=∠E.
在△ABC 和△AED 中,$\begin{cases} AB=AE, \\ ∠B=∠E, \\ BC=ED, \end{cases}$
∴△ABC≌△AED(SAS).
∴AC=AD.
∴∠ACD=∠ADC.
∵五边形 ABCDE 为正五边形,
∴AB=AE=BC=ED,∠B=∠E.
在△ABC 和△AED 中,$\begin{cases} AB=AE, \\ ∠B=∠E, \\ BC=ED, \end{cases}$
∴△ABC≌△AED(SAS).
∴AC=AD.
∴∠ACD=∠ADC.
6. (6 分)图(1)是我们常见的地砖上的图案, 其中包含了一种特殊的平面图形——正八边形. 如图(2), $ AE $ 是 $ \odot O $ 的直径, 请你用直尺和圆规作 $ \odot O $ 的内接正八边形 $ ABCDEFGH $. (不写作法, 保留作图痕迹)


答案:
解:如图,正八边形 ABCDEFGH 即为所求.

解:如图,正八边形 ABCDEFGH 即为所求.

7. (3 分)如图, 正方形 $ ABCD $ 内接于 $ \odot O $, 点 $ P $ 在 $ \overset{\frown}{AB} $ 上, 则 $ \angle BPC $ 的度数为 (

A.$ 30^{\circ} $
B.$ 45^{\circ} $
C.$ 60^{\circ} $
D.$ 90^{\circ} $
B
)
A.$ 30^{\circ} $
B.$ 45^{\circ} $
C.$ 60^{\circ} $
D.$ 90^{\circ} $
答案:
B
查看更多完整答案,请扫码查看


