第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. (3分)(2025·梧州藤县期末)若四边形 $ABCD$ 是 $\odot O$ 的内接四边形, $\angle A:\angle C = 1:2$, 则 $\angle C$ 的度数为 (
A.$120^{\circ}$
B.$130^{\circ}$
C.$140^{\circ}$
D.$150^{\circ}$
A
)A.$120^{\circ}$
B.$130^{\circ}$
C.$140^{\circ}$
D.$150^{\circ}$
答案:
A
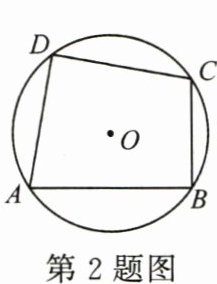
2. (3分)如图, 四边形 $ABCD$ 内接于 $\odot O$, 若 $\angle A = 80^{\circ}$, 则 $\angle C$ 的度数为 (
A.$80^{\circ}$
B.$100^{\circ}$
C.$110^{\circ}$
D.$120^{\circ}$
B
)
A.$80^{\circ}$
B.$100^{\circ}$
C.$110^{\circ}$
D.$120^{\circ}$
答案:
B
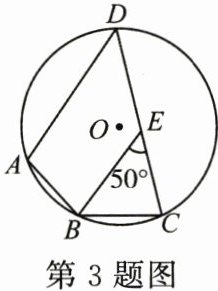
3. (3分)(2024·吉林中考)如图, 四边形 $ABCD$ 内接于 $\odot O$.过点 $B$ 作 $BE // AD$, 交 $CD$ 于点 $E$. 若 $\angle BEC = 50^{\circ}$, 则 $\angle ABC$ 的度数为 (
A.$50^{\circ}$
B.$100^{\circ}$
C.$130^{\circ}$
D.$150^{\circ}$
C
)
A.$50^{\circ}$
B.$100^{\circ}$
C.$130^{\circ}$
D.$150^{\circ}$
答案:
C
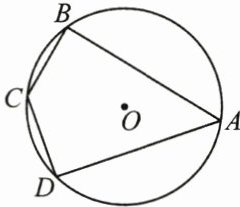
4. (3分)(2024·青海中考)如图, 四边形 $ABCD$ 是 $\odot O$ 的内接四边形, $\angle A = 50^{\circ}$, 则 $\angle C$ 的度数为
130°
.
答案:
130°
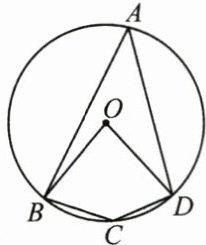
5. (3分)如图, 已知四边形 $ABCD$ 是 $\odot O$ 的内接四边形, $\angle BOD = 80^{\circ}$, 则 $\angle BCD$ 的度数为
140°
.
答案:
140°
6. (8分)如图, 四边形 $ABCD$ 是 $\odot O$ 的内接四边形, $AD$ 与 $BC$ 的延长线交于点 $E$, $\angle DCB = 100^{\circ}$, $\angle B = 50^{\circ}$. 求证: $\triangle CDE$ 是等腰三角形.
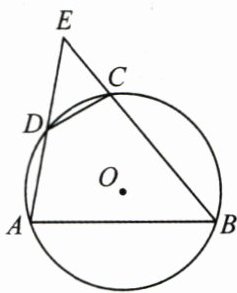

答案:
证明:
∵四边形ABCD是⊙O的内接四边形,
∴∠CDA+∠B=180°.
∵∠B=50°,
∴∠CDA=180°-50°=130°.
∴∠CDE=180°-∠CDA=180°-130°=50°.
∵∠DCB=100°,
∴∠CDE+∠E=100°.
∴∠E=50°.
∴∠E=∠CDE.
∴CD=CE.
∴△CDE是等腰三角形.
∵四边形ABCD是⊙O的内接四边形,
∴∠CDA+∠B=180°.
∵∠B=50°,
∴∠CDA=180°-50°=130°.
∴∠CDE=180°-∠CDA=180°-130°=50°.
∵∠DCB=100°,
∴∠CDE+∠E=100°.
∴∠E=50°.
∴∠E=∠CDE.
∴CD=CE.
∴△CDE是等腰三角形.
7. (3分)如图, 四边形 $ABCD$ 内接于 $\odot O$, $P$ 为边 $AD$ 上任意一点(点 $P$ 不与点 $A$, $D$ 重合), 连接 $CP$.若 $\angle B = 120^{\circ}$, 则 $\angle APC$ 的度数可能为 (
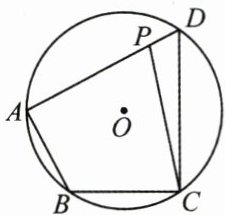
A.$30^{\circ}$
B.$45^{\circ}$
C.$50^{\circ}$
D.$65^{\circ}$
D
)
A.$30^{\circ}$
B.$45^{\circ}$
C.$50^{\circ}$
D.$65^{\circ}$
答案:
D
查看更多完整答案,请扫码查看


