第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1.(3分)(2025·南京鼓楼区质检)已知△ABC中,AB = AC,若以点A为圆心,以AB为半径作圆,则点C在⊙A(
A.内
B.上
C.外
D.内或外
B
)A.内
B.上
C.外
D.内或外
答案:
B
2.(3分)已知点P不在⊙O上,若点P到⊙O上的点的最小距离是4cm,最大距离是9cm,则⊙O的半径是
6.5 cm 或 2.5 cm
.
答案:
6.5 cm 或 2.5 cm
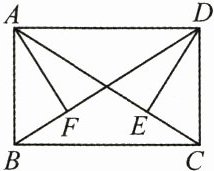
3.(6分)(2025·庆阳镇原县期末)如图,在矩形ABCD中,AB = 3,AD = 4.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF,AE的长;
(2)若以点A为圆心作圆,B,C,D,E,F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.
(1)求AF,AE的长;
(2)若以点A为圆心作圆,B,C,D,E,F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.

答案:
解:
(1)
∵在矩形 ABCD 中,AB = 3,AD = 4,
∴AC = BD = √(3² + 4²) = 5.
∵(1/2)AF·BD = (1/2)AB·AD,
∴AF = (3×4)/5 = 12/5.
同理可得 DE = 12/5.
在 Rt△ADE 中,AE = √(4² - (12/5)²) = 16/5.
(2)
∵AF < AB < AE < AD < AC,
∴若以点 A 为圆心作圆,B,C,D,E,F 五点中至少有 1 个点在圆内,且至少有 2 个点在圆外,即点 F 在圆内,点 D,C 在圆外.
∴⊙A 的半径 r 的取值范围为 2.4 < r < 4.
(1)
∵在矩形 ABCD 中,AB = 3,AD = 4,
∴AC = BD = √(3² + 4²) = 5.
∵(1/2)AF·BD = (1/2)AB·AD,
∴AF = (3×4)/5 = 12/5.
同理可得 DE = 12/5.
在 Rt△ADE 中,AE = √(4² - (12/5)²) = 16/5.
(2)
∵AF < AB < AE < AD < AC,
∴若以点 A 为圆心作圆,B,C,D,E,F 五点中至少有 1 个点在圆内,且至少有 2 个点在圆外,即点 F 在圆内,点 D,C 在圆外.
∴⊙A 的半径 r 的取值范围为 2.4 < r < 4.
4.(3分)(2025·宁波余姚市质检)如图,已知点O是△ABC的外心,∠A = 50°,连接BO,CO,则∠BOC的度数是(
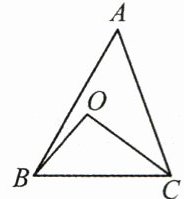
A.90°
B.100°
C.110°
D.95°
B
)
A.90°
B.100°
C.110°
D.95°
答案:
B
5.(3分)如图,⊙O的半径为1,△ABC内接于⊙O.若∠A = 60°,∠B = 75°,则AB =
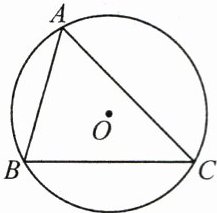
√2
.
答案:
√2
6.(6分)如图,△ABC内接于⊙O,AB是直径,弦CE⊥AB于点F,C是$\overset{\frown}{AD}$的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE,BC于点P,Q.求证:点P是△ACQ的外心.
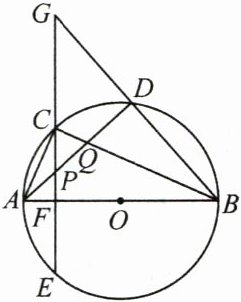

答案:
证明:
∵C 是⌢AD的中点,
∴⌢AC = ⌢CD.
∴∠CAD = ∠ABC.
∵AB 是⊙O 的直径,
∴∠ACB = 90°.
∴∠CAD + ∠AQC = 90°.
又
∵CE⊥AB,
∴∠ABC + ∠PCQ = 90°.
∴∠AQC = ∠PCQ.
∴PC = PQ.
∵CE⊥AB,
∴⌢AC = ⌢AE.
∴⌢AE = ⌢CD.
∴∠CAD = ∠ACE.
∴PA = PC.
∴PA = PC = PQ.
∴点 P 是△ACQ 的外心.
∵C 是⌢AD的中点,
∴⌢AC = ⌢CD.
∴∠CAD = ∠ABC.
∵AB 是⊙O 的直径,
∴∠ACB = 90°.
∴∠CAD + ∠AQC = 90°.
又
∵CE⊥AB,
∴∠ABC + ∠PCQ = 90°.
∴∠AQC = ∠PCQ.
∴PC = PQ.
∵CE⊥AB,
∴⌢AC = ⌢AE.
∴⌢AE = ⌢CD.
∴∠CAD = ∠ACE.
∴PA = PC.
∴PA = PC = PQ.
∴点 P 是△ACQ 的外心.
查看更多完整答案,请扫码查看


