第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. (3分)(2025·三亚质检)二次函数$ y = ax^{2}+bx $,当$ x = 1 $时,$ y = 2 $;当$ x = - 1 $时,$ y = 4 $,则$ a $,$ b $的值是 (
A.$ a = 3 $,$ b = - 1 $
B.$ a = 3 $,$ b = 1 $
C.$ a = - 3 $,$ b = 1 $
D.$ a = - 3 $,$ b = - 1 $
A
)A.$ a = 3 $,$ b = - 1 $
B.$ a = 3 $,$ b = 1 $
C.$ a = - 3 $,$ b = 1 $
D.$ a = - 3 $,$ b = - 1 $
答案:
A
2. (3分)(2025·菏泽牡丹区模拟)已知$ y $关于$ x $的二次函数的图象经过原点及点( - 1,-1),且图象与$ x $轴的另一个交点在原点左侧,到原点的距离为2,那么该二次函数的解析式为
$y=x^{2}+2x$
.
答案:
$y=x^{2}+2x$
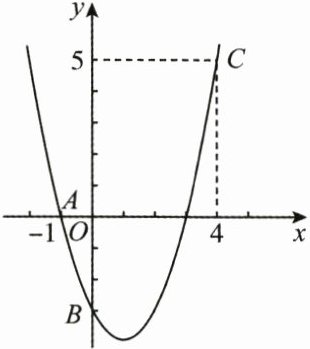
3. (6分)(2025·泉州质检)如图,二次函数$ y = ax^{2}+bx + c 的图象经过 A $,$ B $,$ C $三点.
(1)观察图象写出$ A $,$ B $,$ C $三点的坐标,并求出此二次函数的解析式;
(2)求出此抛物线的顶点坐标和对称轴.
(1)观察图象写出$ A $,$ B $,$ C $三点的坐标,并求出此二次函数的解析式;
(2)求出此抛物线的顶点坐标和对称轴.

答案:
解:
(1)根据二次函数的图象可知
$A(-1,0)$,$B(0,-3)$,$C(4,5)$.
把$A(-1,0)$,$B(0,-3)$,$C(4,5)$代入$y=ax^{2}+bx+c$,得$\left\{\begin{array}{l} a - b + c = 0\\ c = -3\\ 16a + 4b + c = 5\end{array}\right. $
解得$\left\{\begin{array}{l} a = 1\\ b = -2\\ c = -3\end{array}\right. $
$\therefore$二次函数的解析式为$y=x^{2}-2x-3$.
(2)$\because y=x^{2}-2x-3=(x - 1)^{2}-4$,
$\therefore$此抛物线的顶点坐标为$(1,-4)$,对称轴为直线$x = 1$.
(1)根据二次函数的图象可知
$A(-1,0)$,$B(0,-3)$,$C(4,5)$.
把$A(-1,0)$,$B(0,-3)$,$C(4,5)$代入$y=ax^{2}+bx+c$,得$\left\{\begin{array}{l} a - b + c = 0\\ c = -3\\ 16a + 4b + c = 5\end{array}\right. $
解得$\left\{\begin{array}{l} a = 1\\ b = -2\\ c = -3\end{array}\right. $
$\therefore$二次函数的解析式为$y=x^{2}-2x-3$.
(2)$\because y=x^{2}-2x-3=(x - 1)^{2}-4$,
$\therefore$此抛物线的顶点坐标为$(1,-4)$,对称轴为直线$x = 1$.
4. (3分)(2025·广安质检)抛物线的对称轴为直线$ x = 3 $,$ y 的最大值为 - 5 $,且与$ y= \frac{1}{2}x^{2} $的图象开口大小相同,则这条抛物线的函数解析式为 (
A.$ y = - \frac{1}{2}(x + 3)^{2}+5 $
B.$ y = - \frac{1}{2}(x - 3)^{2}-5 $
C.$ y = \frac{1}{2}(x + 3)^{2}+5 $
D.$ y = \frac{1}{2}(x - 3)^{2}-5 $
B
)A.$ y = - \frac{1}{2}(x + 3)^{2}+5 $
B.$ y = - \frac{1}{2}(x - 3)^{2}-5 $
C.$ y = \frac{1}{2}(x + 3)^{2}+5 $
D.$ y = \frac{1}{2}(x - 3)^{2}-5 $
答案:
B
5. (3分)(2025·铁岭昌图县模拟)如图是一条抛物线,则其函数解析式为 (
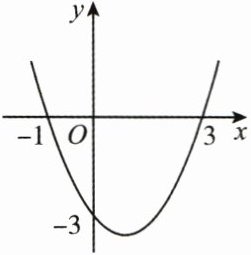
A.$ y = x^{2}-2x + 3 $
B.$ y = x^{2}-2x - 3 $
C.$ y = x^{2}+2x + 3 $
D.$ y = x^{2}+2x - 3 $
B
)
A.$ y = x^{2}-2x + 3 $
B.$ y = x^{2}-2x - 3 $
C.$ y = x^{2}+2x + 3 $
D.$ y = x^{2}+2x - 3 $
答案:
B
6. (3分)已知抛物线过点$ A(2,0) $,$ B( - 1,0) $,与$ y 轴交于点 C $,且$ OC = 2 $,则这条抛物线的函数解析式为
$y=x^{2}-x-2$或$y=-x^{2}+x+2$
.
答案:
$y=x^{2}-x-2$或$y=-x^{2}+x+2$
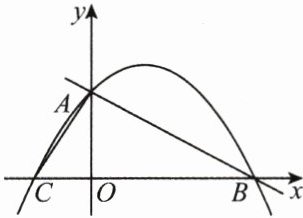
7. (9分)(2025·张掖甘州期末)如图,在直角坐标系中,已知直线$ y = - \frac{1}{2}x + 4 与 y 轴交于点 A $,与$ x 轴交于点 B $,点$ C 的坐标为( - 2,0) $.
(1)求经过$ A $,$ B $,$ C $三点的抛物线的函数解析式;
(2)如果$ M $为抛物线的顶点,连接$ AM $,$ BM $,求四边形$ AOBM $的面积.
(1)求经过$ A $,$ B $,$ C $三点的抛物线的函数解析式;
(2)如果$ M $为抛物线的顶点,连接$ AM $,$ BM $,求四边形$ AOBM $的面积.

答案:
解:
(1)当$x = 0$时,$y=-\dfrac {1}{2}x + 4 = 4$,则$A(0,4)$.
当$y = 0$时,$-\dfrac {1}{2}x + 4 = 0$,解得$x = 8$,则$B(8,0)$.
设抛物线的函数解析式为$y=a(x + 2)(x - 8)$.把$A(0,4)$代入,得$a\cdot 2\cdot (-8)=4$,
解得$a=-\dfrac {1}{4}$.
$\therefore$抛物线的函数解析式为$y=-\dfrac {1}{4}(x + 2)(x - 8)$,即$y=-\dfrac {1}{4}x^{2}+\dfrac {3}{2}x + 4$.
(2)$\because y=-\dfrac {1}{4}x^{2}+\dfrac {3}{2}x + 4=-\dfrac {1}{4}(x - 3)^{2}+\dfrac {25}{4}$,
$\therefore M\left(3,\dfrac {25}{4}\right)$.
如图,作$MD\perp x$轴于点$D$,

$\therefore S_{四边形AOBM}=S_{梯形AODM}+S_{\triangle BDM}$
$=\dfrac {1}{2}× \left(4+\dfrac {25}{4}\right)× 3+\dfrac {1}{2}× 5× \dfrac {25}{4}$
$=31$.
解:
(1)当$x = 0$时,$y=-\dfrac {1}{2}x + 4 = 4$,则$A(0,4)$.
当$y = 0$时,$-\dfrac {1}{2}x + 4 = 0$,解得$x = 8$,则$B(8,0)$.
设抛物线的函数解析式为$y=a(x + 2)(x - 8)$.把$A(0,4)$代入,得$a\cdot 2\cdot (-8)=4$,
解得$a=-\dfrac {1}{4}$.
$\therefore$抛物线的函数解析式为$y=-\dfrac {1}{4}(x + 2)(x - 8)$,即$y=-\dfrac {1}{4}x^{2}+\dfrac {3}{2}x + 4$.
(2)$\because y=-\dfrac {1}{4}x^{2}+\dfrac {3}{2}x + 4=-\dfrac {1}{4}(x - 3)^{2}+\dfrac {25}{4}$,
$\therefore M\left(3,\dfrac {25}{4}\right)$.
如图,作$MD\perp x$轴于点$D$,

$\therefore S_{四边形AOBM}=S_{梯形AODM}+S_{\triangle BDM}$
$=\dfrac {1}{2}× \left(4+\dfrac {25}{4}\right)× 3+\dfrac {1}{2}× 5× \dfrac {25}{4}$
$=31$.
查看更多完整答案,请扫码查看


