第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
8. (3分)(2025·德州陵城区质检)有一个圆的半径为5,则该圆的弦长不可能是 (
A.1
B.4
C.10
D.11
D
)A.1
B.4
C.10
D.11
答案:
D
9. (3分)(2025·台州仙居县模拟)如果一个平行四边形的四边的中点都在同一个圆上,那么这个四边形的对角线具有的性质是 (
A.互相平分但不一定垂直
B.互相平分且相等
C.互相垂直平分
D.互相垂直但不一定互相平分
B
)A.互相平分但不一定垂直
B.互相平分且相等
C.互相垂直平分
D.互相垂直但不一定互相平分
答案:
B
10. (3分)(2025·德州宁津县期中)如图,在$\triangle ABC$中,$AB为\odot O$的直径,$\angle B = 60^{\circ}$,$\angle BOD = 100^{\circ}$,则$\angle C$的度数为 (
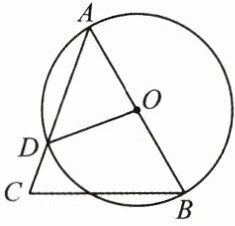
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
C
)
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
答案:
C
11. (3分)如图,圆中以$A$为一个端点的劣弧有
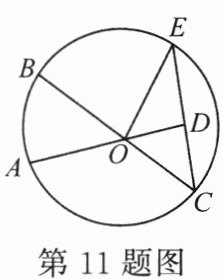
3
条.
答案:
3
12. (3分)(2025·秦皇岛海港区质检)如图,$\odot O的周长为4\pi$,$B是弦CD$上任意一点(与点$C$,$D$不重合),过点$B作OC的平行线交OD于点E$,则$EO + EB = $
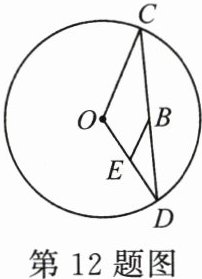
2
.(用数字表示)
答案:
2
13. (6分)如图,$AB是\odot O$的直径,$CD是\odot O$的弦,$AB$,$CD的延长线交于点E$,若$AB = 2DE$,$\angle C = 40^{\circ}$,求$\angle E及\angle AOC$的度数.
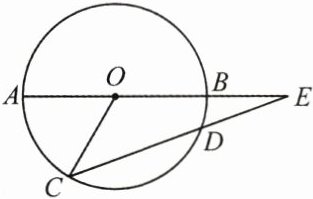

答案:
解:如图,连接OD.
∵OC=OD,∠C=40°,
∴∠ODC=∠C=40°.
∵AB=2DE,OD=$\frac {1}{2}$AB,
∴OD=DE.
∵∠ODC是△DOE的外角,
∴∠E=∠EOD=$\frac {1}{2}$∠ODC=20°.
∵∠AOC是△COE的外角,
∴∠AOC=∠C+∠E=40°+20°=60°.
∵OC=OD,∠C=40°,
∴∠ODC=∠C=40°.
∵AB=2DE,OD=$\frac {1}{2}$AB,
∴OD=DE.
∵∠ODC是△DOE的外角,
∴∠E=∠EOD=$\frac {1}{2}$∠ODC=20°.
∵∠AOC是△COE的外角,
∴∠AOC=∠C+∠E=40°+20°=60°.
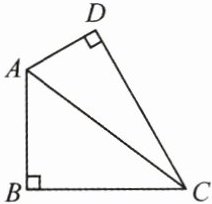
14. (8分)(2025·湛江质检)如图,在四边形$ABCD$中,$\angle ABC$,$\angle ADC$均为直角,且$AB = 3$,$BC = 4$,$AD = 2$.
(1)求证:$A$,$B$,$C$,$D$四个点都在同一个圆上;
(2)求这个圆的半径,并计算它的面积.
(1)求证:$A$,$B$,$C$,$D$四个点都在同一个圆上;
(2)求这个圆的半径,并计算它的面积.

答案:
(1)证明:如图,作△ABC斜边AC的中线BE,连接DE.
∵∠ABC,∠ADC均为直角,
∴△ABC和△ADC均为直角三角形.
∴AE=BE=CE=DE.
∴A,B,C,D四个点都在以点E为圆心的同一个圆上.
(2)解:在Rt△ABC中,AC=$\sqrt {AB^{2}+BC^{2}}$=5,
∴该圆的半径R为$\frac {5}{2}$.
∴圆的面积S=πR²=$\frac {25}{4}$π.
(1)证明:如图,作△ABC斜边AC的中线BE,连接DE.
∵∠ABC,∠ADC均为直角,
∴△ABC和△ADC均为直角三角形.
∴AE=BE=CE=DE.
∴A,B,C,D四个点都在以点E为圆心的同一个圆上.
(2)解:在Rt△ABC中,AC=$\sqrt {AB^{2}+BC^{2}}$=5,
∴该圆的半径R为$\frac {5}{2}$.
∴圆的面积S=πR²=$\frac {25}{4}$π.
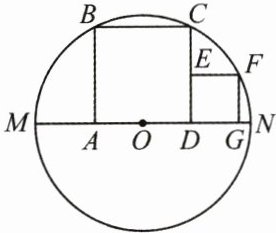
15. (8分)如图,已知$MN为\odot O$的直径,四边形$ABCD$,$EFGD$均是正方形,点$B$,$C$,$F在\odot O$上,点$E在CD$上,点$A$,$D$,$G在MN$上,若正方形$EFGD$的面积为16,求$\odot O的半径r$.

答案:
解:如图,连接OC,OF,设AD=2x.
∵CO²=DO²+CD²,
∴r²=x²+(2x)².
∵OF²=OG²+FG²,
∴r²=(x+4)²+4²=x²+8x+32.
∴x²+(2x)²=x²+8x+32,
解得x₁=4,x₂=-2(舍去).
∴r²=5×4²,r=4$\sqrt {5}$.
∵CO²=DO²+CD²,
∴r²=x²+(2x)².
∵OF²=OG²+FG²,
∴r²=(x+4)²+4²=x²+8x+32.
∴x²+(2x)²=x²+8x+32,
解得x₁=4,x₂=-2(舍去).
∴r²=5×4²,r=4$\sqrt {5}$.
查看更多完整答案,请扫码查看


