《2025年初中同步练习册分层卷九年级数学上册人教版》

7. (3分)(2025·武汉期中)俗语有云:"一天不练手脚慢,两天不练丢一半,三天不练门外汉,四天不练瞪眼看."其意思是知识和技艺在学习后,如果不及时复习,那么学习过的东西就会被遗忘.假设每天"遗忘"的百分比为$x$,根据"两天不练丢一半",可列方程为(A)
A.$(1-x)^{2}= 50\%$
B.$(1+x)^{2}= 50\%$
C.$1-2x= 50\%$
D.$(1-x)(1+x)= 50\%$

答案： A

8. (3分)(2025·邵阳期中)某专卖店销售一种机床,3月每台售价为2万元,共销售60台.根据市场调查,这种机床每台售价每增加0.1万元,就会少售出1台.4月该专卖店想将销售额提高25%,则这种机床每台的售价应定为(D)
A.3万元
B.5万元
C.8万元
D.3万元或5万元

答案： D

9. (3分)(2024·绵阳中考)超市销售某种礼盒,该礼盒的原价为500元.因销量持续攀升,商家在3月提价20%,后发现销量锐减,于是经过核算决定在3月售价的基础上,4,5月按照相同的降价率$r$连续降价.已知5月礼盒的售价为486元,则$r= $10%.

答案： 10%

10. (10分)(2024·辽宁中考)某商场出售一种商品,经市场调查发现,日销售量$y$(件)与每件售价$x$(元)之间满足一次函数关系,部分数据如表所示:

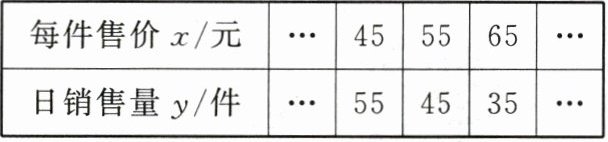
(1)求$y关于x$的函数解析式.(不要求写出自变量$x$的取值范围)
(2)该商品日销售额能否达到2600元?如果能,求出每件售价;如果不能,说明理由.

答案：
(1)解：由题意，设一次函数的解析式为y=kx+b.
把(45，55)，(55，45)代入，得
{45k+b=55，
55k+b=45，
解得{k=-1，
b=100.
∴函数解析式为y=-x+100.
(2)不能.理由如下：
由题意，销售额=x(-x+100)=-x²+100x.
又
∵销售额是2600元，
∴2600=-x²+100x.
∴x²-100x+2600=0.
∵Δ=(-100)²-4×2600=10000-10400=-400＜0，
∴方程无解，故该商品日销售额不能达到2600元.

11. (12分)(2024·淄博中考)"我运动,我健康,我快乐!"随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2021年的32万人增加到2023年的50万人.
(1)求该市参加健身运动人数的年均增长率.
(2)为支持市民的健身运动,市政府决定从A公司购买某种套装健身器材.该公司规定:若购买不超过100套,每套售价1600元;若超过100套,每增加10套,每套售价可降低40元,但最低售价不得低于1000元.已知市政府向该公司支付货款24万元,求购买的这种健身器材的套数.

答案：
(1)解：设该市参加健身运动人数的年均增长率为x.
由题意，得32(1+x)²=50，
解得x₁=0.25=25%，x₂=-2.25(不符合题意，舍去).
答：该市参加健身运动人数的年均增长率为25%.
(2)解：设购买的这种健身器材为m套.
由题意，得m(1600-$\frac{m-100}{10}$×40)=240000.
整理，得m²-500m+60000=0，
解得m₁=200，m₂=300.
当m=200时，1600-$\frac{m-100}{10}$×40=1200＞1000，符合题意；
当m=300时，1600-$\frac{m-100}{10}$×40=800＜1000，不符合题意，舍去.
答：购买的这种健身器材为200套.