《2025年初中同步练习册分层卷九年级数学上册人教版》

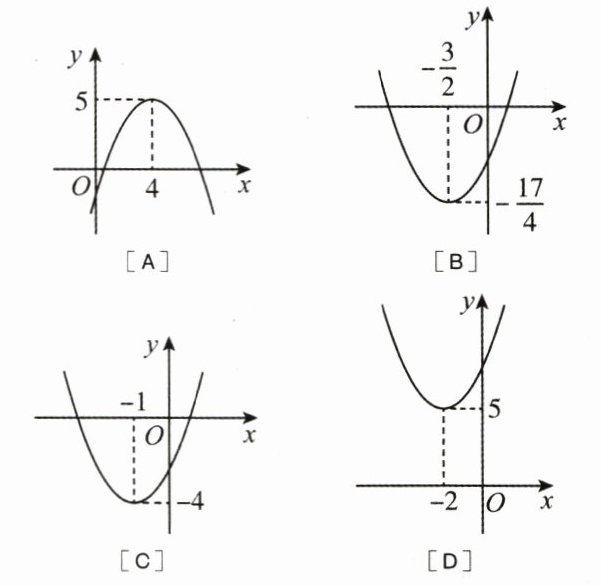
1. (3 分)(2025·德州临邑县期末)二次函数 $ y = x^2 + 3x - 2 $ 的图象是 (B)

答案： B

2. (3 分)(2025·遵化模拟)对于抛物线 $ y = -2x^2 + 4x + 1 $,下列判断正确的是(C)
A.抛物线的开口向上
B.抛物线的顶点坐标是$(-1, 3)$
C.对称轴为直线 $ x = 1 $
D.当 $ x = 3 $ 时,$ y ＞ 0 $

答案： C

3. (3 分)已知二次函数 $ y = x^2 - 4x + 2 $,当 $ -1 \leq x \leq 3 $ 时,下列正确说法的序号是 ④.
①有最大值$-1$,有最小值$-2$；②有最大值 $ 0 $,有最小值$-1$；③有最大值 $ 7 $,有最小值$-1$；④有最大值 $ 7 $,有最小值$-2$.

答案： ④

4. (6 分)(2025·随州曾都区期中)已知二次函数 $ y = \frac{1}{2}x^2 - 3x + 4 $.
(1)配方成 $ y = a(x - h)^2 + k $ 的形式；
(2)求出它的图象的开口方向、对称轴和顶点坐标；
(3)求当 $ y ＜ 0 $ 时,$ x $ 的取值范围.

答案：
(1)二次函数$y=\frac{1}{2}x^{2}-3x+4=\frac{1}{2}(x-3)^{2}-\frac{1}{2}$.
(2)$\because y=\frac{1}{2}(x-3)^{2}-\frac{1}{2}$中$a=\frac{1}{2}＞0$，$\therefore$该函数的开口向上，对称轴是直线$x=3$，顶点坐标为$\left(3,-\frac{1}{2}\right)$.
(3)当$y=0$时，$0=\frac{1}{2}x^{2}-3x+4$，解得$x=2$或$x=4$，且图象开口向上，故当$y＜0$时，$x$的取值范围是$2＜x＜4$.

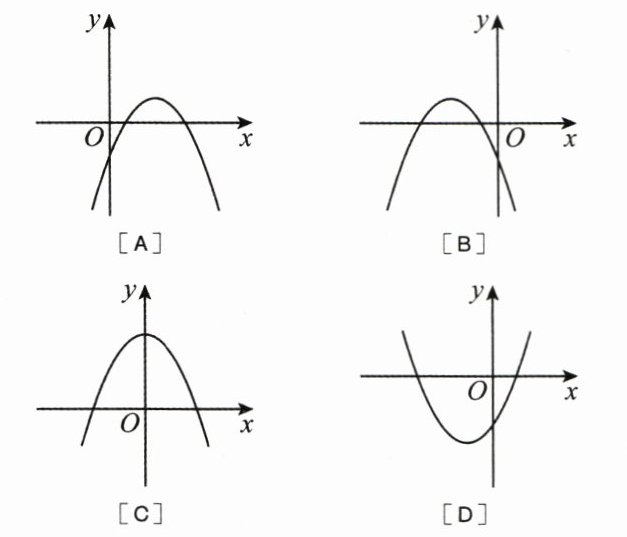
5. (3 分)(2025·肇庆德庆县模拟)如图,$ a ＜ 0 $,$ b ＞ 0 $,$ c ＜ 0 $,那么二次函数 $ y = ax^2 + bx + c $ 的图象可能是 (A)

答案： A

6. (8 分)(2025·烟台栖霞市期中)已知抛物线 $ y = -x^2 + 2mx - m^2 + 3m + 1 $($ m $ 为常数).
(1)当抛物线的顶点在第二象限时,求 $ m $ 的取值范围；
(2)当 $ -2 \leq x \leq 1 $ 时,$ y $ 先随 $ x $ 的增大而增大,后随 $ x $ 的增大而减小,且当 $ x = 1 $ 时 $ y $ 有最小值,求整数 $ m $ 的值.

答案：
(1)$\because y=-x^{2}+2mx-m^{2}+3m+1=-(x-m)^{2}+3m+1$，$\therefore$抛物线的顶点为$(m,3m+1)$.$\because$抛物线的顶点在第二象限，$\therefore \begin{cases} m＜0, \\ 3m+1＞0, \end{cases}$解得$-\frac{1}{3}＜m＜0$.
(2)$\because$抛物线的对称轴为直线$x=m$，且当$-2\leqslant x\leqslant1$时，$y$先随$x$的增大而增大，后随$x$的增大而减小，$\therefore -2＜m＜1$.当$x=-2$时，$y=-m^{2}-m-3$；当$x=1$时，$y=-m^{2}+5m$.$\because$当$x=1$时$y$有最小值，$\therefore -m^{2}+5m\leqslant -m^{2}-m-3$，解得$m\leqslant -\frac{1}{2}$.综上所述，$-2＜m\leqslant -\frac{1}{2}$.$\therefore$整数$m$的值为$-1$.