《2025年初中同步练习册分层卷九年级数学上册人教版》

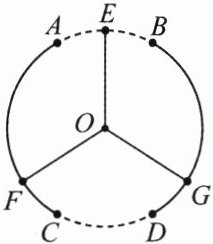
9. (3 分)(2025·台州仙居县期末)某酒店的圆形旋转门可看成由外围的$\odot O$和三翼隔风玻璃组成(示意图如图所示),外围圆有通道弧$AB和弧CD$,且它们关于圆心$O$中心对称,圆内的三翼隔风玻璃可绕圆心$O$转动,且所成的夹角$∠EOF = ∠FOG = ∠GOE = 120^{\circ}$,三翼隔风玻璃在转动过程中,始终使大厅内外空气隔离,起到对大厅内的保温作用.例如,当隔风玻璃转到如图所示位置时,大厅内外空气被隔风玻璃$OF$,$OG$隔离.通道弧$AB$所对圆心角的度数的最大值为 (B)

A.$30^{\circ}$
B.$60^{\circ}$
C.$90^{\circ}$
D.$120^{\circ}$

答案： B

10. (3 分)(2025·淮安金湖县期末)长度等于$6\sqrt{2}的弦所对的圆心角是90^{\circ}$,则该圆的半径为$6$.

答案： 6

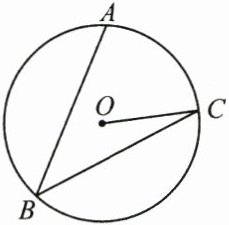
11. (3 分)(2025·杭州一模)如图,点A,B,C在$\odot O$上,分别连接AB,BC,OC.若$AB = BC,∠B = 40^{\circ},$则∠OCB的度数为20°.

答案： 20°

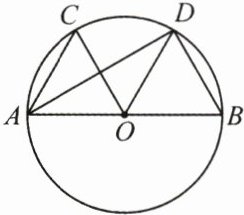
12. (10 分)(2025·绍兴嵊州市期中)如图,$AB是\odot O$的直径,$\overset{\frown}{AC}= \overset{\frown}{CD}$,$∠COD = 60^{\circ}$.
(1)$\triangle AOC$是等边三角形吗？请说明理由.
(2)求证：$OC// BD$.

答案：
(1)解：△AOC是等边三角形.理由如下：
∵$\overset{\frown}{AC}=\overset{\frown}{CD}$，
∴∠AOC=∠COD=60°.
∵OA=OC，
∴△AOC是等边三角形.
(2)证明：
∵∠AOC=∠COD=60°，
∴∠DOB=60°.
又
∵OB=OD，
∴△OBD为等边三角形.
∴∠B=60°.
∴∠AOC=∠B.
∴OC//BD.

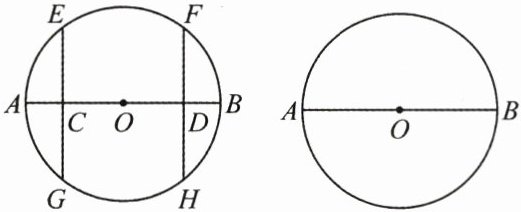
13. (14 分)如图,在$\odot O$中,$C$,$D是直径AB$上的两点,且$AC = BD$,$EG\perp AB于点C$,$FH\perp AB于点D$,点$E$,$G$,$F$,$H在\odot O$上.
(1)若$EG = 8$,$AC = 2$,求$\odot O$的半径；
(2)求证：$\overset{\frown}{AE}= \overset{\frown}{BF}$；
(3)若$C$,$D分别为OA$,$OB$的中点,则$\overset{\frown}{AE}= \overset{\frown}{EF}= \overset{\frown}{FB}$成立吗？请说明理由.

答案：
(1)解：如图，连接EO.
设$\odot O$的半径为r.
∵EG⊥AB，
∴CE=CG=$\frac{1}{2}$EG=4.
∵AC=2，
∴OC=r-2.
在Rt△CEO中，OE²=CE²+OC²，
∴r²=4²+(r-2)²，解得r=5.
∴$\odot O$的半径为5.
(2)证明：如图，连接OF.
∵AC=BD，OA=OB，
∴OC=OD.
∵EG⊥AB，FH⊥AB，
∴在Rt△COE和Rt△DOF中，$\left\{\begin{array}{l} OC=OD,\\ OE=OF.\end{array}\right. $
∴Rt△COE≌Rt△DOF(HL).
∴∠AOE=∠BOF.
∴$\overset{\frown}{AE}=\overset{\frown}{BF}$.
(3)解：$\overset{\frown}{AE}=\overset{\frown}{EF}=\overset{\frown}{FB}$成立.理由如下：
∵C，D分别为OA，OB的中点，
∴OC=$\frac{1}{2}$OE.
∴∠OEC=30°.
∴∠AOE=60°.
同理∠BOF=60°，
∴∠EOF=60°.
∴$\overset{\frown}{AE}=\overset{\frown}{EF}=\overset{\frown}{FB}$.