《2025年初中同步练习册分层卷九年级数学上册人教版》

1. (3分)(2025·运城期末)图(1)是一只葡萄酒杯,酒杯的上半部分是以抛物线为模型设计而成,且是轴对称图形.从正面看葡萄酒杯的上半部分是一条抛物线,若 $ AB = 4 $,$ CD = 3 $,以顶点 $ C $ 为原点建立如图(2)所示的平面直角坐标系,则抛物线的函数解析式为 (A)

A.$ y = \frac{3}{4}x^2 $
B.$ y = \frac{3}{16}x^2 $
C.$ y = -\frac{3}{4}x^2 $
D.$ y = -\frac{3}{16}x^2 $

答案： A

2. (3分)(2025·宜春高安市期中)廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数解析式为 $ y = -\frac{1}{40}x^2 + 10 $,为保护廊桥的安全,在该抛物线上距水面 $ AB $ 高为 $ 8 $ m 的点 $ E $,$ F $ 处要安装两盏警示灯,则这两盏灯的水平距离 $ EF $ 是$8\sqrt{5}$m.

答案： $8\sqrt{5}$

3. (12分)图(1)为某新建住宅小区修建的一个横断面为抛物线的拱形大门,点 $ Q $ 为顶点,其高为 $ 6 $ m,宽 $ OP $ 为 $ 12 $ m.以点 $ O $ 为原点、$ OP $ 所在直线为 $ x $ 轴建立直角坐标系.
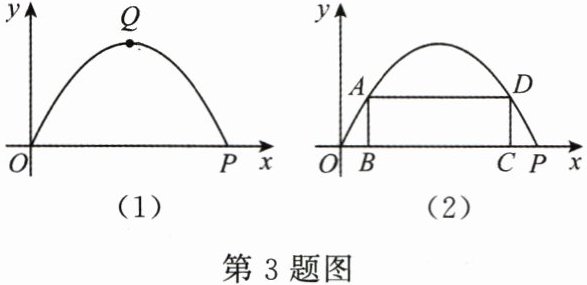
(1)求出该抛物线的函数解析式,并写出自变量 $ x $ 的取值范围.
(2)拱形大门下的道路设双向行车道供车辆出入(正中间是宽 $ 1 $ m 的值班室),其中的一条行车道能否行驶宽 $ 2.5 $ m、高 $ 3.5 $ m 的消防车辆? 请通过计算说明.
(3)如图(2),小区物业计划在拱形大门处安装一个矩形"光带" $ ABCD $,使点 $ A $,$ D $ 在抛物线上,点 $ B $,$ C $ 在 $ OP $ 上,求出所需的三根"光带" $ AB $,$ AD $,$ DC $ 的长度之和的最大值.

答案： 解：
(1)
∵P(12，0)，Q(6，6)，
∴设这条抛物线的函数解析式为$y=a(x-6)^{2}+6$.
∵抛物线过点O(0，0)，
∴$a(0-6)^{2}+6=0$，解得$a=-\frac{1}{6}$.
∴这条抛物线的函数解析式为$y=-\frac{1}{6}(x-6)^{2}+6$，即$y=-\frac{1}{6}x^{2}+2x(0\leqslant x\leqslant 12)$.
(2)
∵当$x=6-0.5-2.5=3$(或$x=6+0.5+2.5=9$)时，$y=4.5＞3.5$，
∴故能行驶宽2.5 m、高3.5 m的消防车辆.
(3)设点A的坐标为$(m,-\frac{1}{6}m^{2}+2m)$，则$OB=m$，$AB=DC=-\frac{1}{6}m^{2}+2m$.根据抛物线的轴对称性，得$CP=OB=m$，则$BC=12-2m$，即$AD=12-2m$.令$L=AB+AD+DC=-\frac{1}{6}m^{2}+2m+12-2m-\frac{1}{6}m^{2}+2m=-\frac{1}{3}m^{2}+2m+12=-\frac{1}{3}(m-3)^{2}+15$，故三根“光带”的长度之和的最大值为15 m.