第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
7. (3分)(2025·广州质检)如图,$ \triangle ABC 与 \triangle A'B'C 关于点 C(0,-1) $成中心对称,若点A的坐标为$ (3,1) $,则点$ A' $的坐标为 (
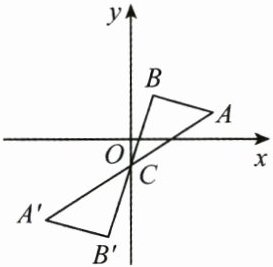
A.$ (-3,-1) $
B.$ (-3,-2) $
C.$ (-3,-3) $
D.$ (-3,-4) $
C
)
A.$ (-3,-1) $
B.$ (-3,-2) $
C.$ (-3,-3) $
D.$ (-3,-4) $
答案:
C
8. (3分)如图,$ □ ABCO 与 □ A'B'C'O $关于点O成中心对称,$ \angle BAO $的平分线交BC于点D,若$ BD = 3 $, $ CD = 2 $,则$ □ A'B'C'O $的周长为
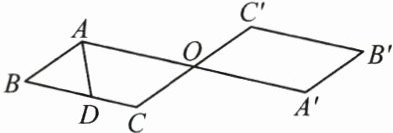
16
.
答案:
16
9. (3分)(2025·德州德城区期末)如图,已知$ \triangle ABC 与 \triangle CDA $关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,下面的结论:①点E和点F、点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤$ \triangle AOE 与 \triangle COF $成中心对称.其中,正确的为
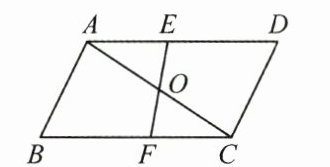
①②③④⑤
.(填序号)
答案:
①②③④⑤
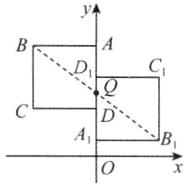
10. (10分)(2025·南昌期中)如图,正方形ABCD与正方形$ A_1B_1C_1D_1 $关于某点中心对称.已知A,$ D_1 $,D三点的坐标分别是$ (0,4) $, $ (0,3) $, $ (0,2) $.
(1)求对称中心Q的坐标,并仅用直尺画出点Q的位置;
(2)写出顶点B,C,$ B_1 $,$ C_1 $的坐标.
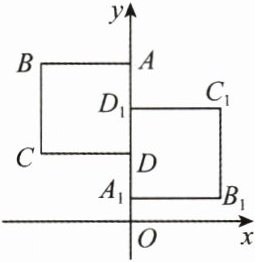
(1)求对称中心Q的坐标,并仅用直尺画出点Q的位置;
(2)写出顶点B,C,$ B_1 $,$ C_1 $的坐标.

答案:
解:
(1)根据对称中心的性质,可得对称中心的坐标是$D_1D$的中点.
∵点$D_1$,D 的坐标分别是$(0,\ 3)$,$(0,\ 2)$,
∴对称中心点 Q 的坐标是$(0,\ 2.5)$.
如图,连接$BB_1$交$AA_1$于点 Q,则点 Q 即为所求.
(2)
∵点 A,D 的坐标分别是$(0,\ 4)$,$(0,\ 2)$,
∴正方形 ABCD 与正方形$A_1B_1C_1D_1$的边长都是$4 - 2 = 2$.
∴B,C 的坐标分别是$(-2,\ 4)$,$(-2,\ 2)$.
∵$A_1D_1 = 2$,$D_1$的坐标是$(0,\ 3)$,
∴$A_1$的坐标是$(0,\ 1)$.
∴$B_1$,$C_1$的坐标分别是$(2,\ 1)$,$(2,\ 3)$.
综上,可得顶点 B,C,$B_1$,$C_1$的坐标分别是$(-2,\ 4)$,$(-2,\ 2)$,$(2,\ 1)$,$(2,\ 3)$.
解:
(1)根据对称中心的性质,可得对称中心的坐标是$D_1D$的中点.
∵点$D_1$,D 的坐标分别是$(0,\ 3)$,$(0,\ 2)$,
∴对称中心点 Q 的坐标是$(0,\ 2.5)$.
如图,连接$BB_1$交$AA_1$于点 Q,则点 Q 即为所求.

(2)
∵点 A,D 的坐标分别是$(0,\ 4)$,$(0,\ 2)$,
∴正方形 ABCD 与正方形$A_1B_1C_1D_1$的边长都是$4 - 2 = 2$.
∴B,C 的坐标分别是$(-2,\ 4)$,$(-2,\ 2)$.
∵$A_1D_1 = 2$,$D_1$的坐标是$(0,\ 3)$,
∴$A_1$的坐标是$(0,\ 1)$.
∴$B_1$,$C_1$的坐标分别是$(2,\ 1)$,$(2,\ 3)$.
综上,可得顶点 B,C,$B_1$,$C_1$的坐标分别是$(-2,\ 4)$,$(-2,\ 2)$,$(2,\ 1)$,$(2,\ 3)$.
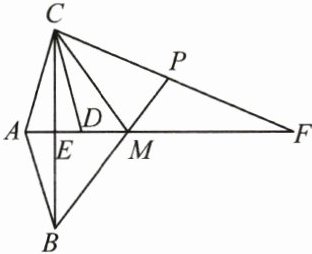
11. (12分)(2025·宿迁质检)如图,$ \triangle ABM 与 \triangle ACM $关于直线AF成轴对称,$ \triangle ABE 与 \triangle DCE $关于点E成中心对称,点E,D,M都在线段AF上,BM的延长线交CF于点P.
(1)求证:$ AC = CD $;
(2)若$ \angle BAC = 2\angle MPC $,请你判断$ \angle F 与 \angle MCD $的数量关系,并说明理由.
(1)求证:$ AC = CD $;
(2)若$ \angle BAC = 2\angle MPC $,请你判断$ \angle F 与 \angle MCD $的数量关系,并说明理由.

答案:
(1)证明:
∵$\triangle ABM$与$\triangle ACM$关于直线 AF 成轴对称,
∴$\triangle ABM\cong\triangle ACM$.
∴$AB = AC$.
又
∵$\triangle ABE$与$\triangle DCE$关于点 E 成中心对称,
∴$\triangle ABE\cong\triangle DCE$.
∴$AB = CD$.
∴$AC = CD$.
(2)解:$\angle F=\angle MCD$.理由如下:
由(1)可得$\angle BAE=\angle CAE=\angle CDE$,$\angle CMA=\angle BMA$.
∵$\angle BAC = 2\angle MPC$,$\angle BMA=\angle PMF$,
∴设$\angle MPC=\alpha$,则$\angle BAE=\angle CAE=\angle CDE=\alpha$.设$\angle BMA=\beta$,则$\angle PMF=\angle CMA=\beta$.
∴$\angle F=\angle MPC - \angle PMF=\alpha - \beta$,$\angle MCD=\angle CDE - \angle DMC=\alpha - \beta$.
∴$\angle F=\angle MCD$.
(1)证明:
∵$\triangle ABM$与$\triangle ACM$关于直线 AF 成轴对称,
∴$\triangle ABM\cong\triangle ACM$.
∴$AB = AC$.
又
∵$\triangle ABE$与$\triangle DCE$关于点 E 成中心对称,
∴$\triangle ABE\cong\triangle DCE$.
∴$AB = CD$.
∴$AC = CD$.
(2)解:$\angle F=\angle MCD$.理由如下:
由(1)可得$\angle BAE=\angle CAE=\angle CDE$,$\angle CMA=\angle BMA$.
∵$\angle BAC = 2\angle MPC$,$\angle BMA=\angle PMF$,
∴设$\angle MPC=\alpha$,则$\angle BAE=\angle CAE=\angle CDE=\alpha$.设$\angle BMA=\beta$,则$\angle PMF=\angle CMA=\beta$.
∴$\angle F=\angle MPC - \angle PMF=\alpha - \beta$,$\angle MCD=\angle CDE - \angle DMC=\alpha - \beta$.
∴$\angle F=\angle MCD$.
查看更多完整答案,请扫码查看


