第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
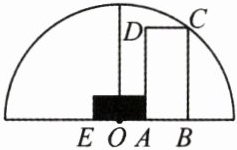
7. (10分)某隧道施工单位准备在双向道路中间全程增加一个宽为1 m的隔离带,已知隧道截面是一个半径为4 m的半圆形,点O是其圆心,AE是隔离带截面,则一辆高3 m、宽1.9 m的卡车ABCD能通过这个隧道吗? 请说明理由.

答案:
解:能通过.理由如下:
如图,连接 OC.

∵OA=$\frac{1}{2}$AE=0.5 m,
∴OB=1.9+0.5=2.4(m).
∴BC=$\sqrt{OC^2-OB^2}=\sqrt{4^2-2.4^2}=3.2$(m)>3 m.
∴一辆高 3 m、宽 1.9 m 的卡车能通过隧道.
解:能通过.理由如下:
如图,连接 OC.

∵OA=$\frac{1}{2}$AE=0.5 m,
∴OB=1.9+0.5=2.4(m).
∴BC=$\sqrt{OC^2-OB^2}=\sqrt{4^2-2.4^2}=3.2$(m)>3 m.
∴一辆高 3 m、宽 1.9 m 的卡车能通过隧道.
8. (3分)(2025·台州温岭市期中)如图,在$5×5$正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是$(-2,4)$,点C的坐标是$(1,3)$,那么这条圆弧所在圆的圆心坐标是 (
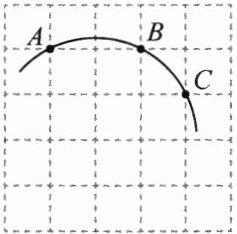
A.$(0,0)$
B.$(-1,2)$
C.$(-1,0)$
D.$(-1,-1)$
B
)
A.$(0,0)$
B.$(-1,2)$
C.$(-1,0)$
D.$(-1,-1)$
答案:
B
9. (3分)(2024·通辽中考)如图,圆形拱门最下端AB在地面上,D为AB的中点,C为拱门最高点,线段CD经过拱门所在圆的圆心,若$AB = 1$ m,$CD = 2.5$ m,则拱门所在圆的半径为 (
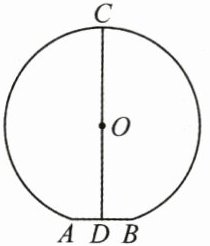
A.1.25 m
B.1.3 m
C.1.4 m
D.1.45 m
B
)
A.1.25 m
B.1.3 m
C.1.4 m
D.1.45 m
答案:
B
10. (3分)如图,已知AB是$\odot O$的弦,C是$\overset{\frown}{AB}$的中点,$AB = 8$,$AC = 2\sqrt{5}$,则$\odot O$半径的长为
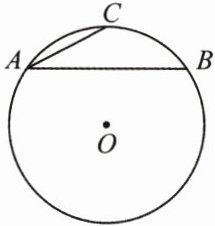
5
.
答案:
5
11. (3分)已知$\odot O$的半径为10 cm,弦$MN// EF$,且$MN = 12$ cm,$EF = 16$ cm,则弦MN和EF之间的距离为____.
答案:
2 cm 或 14 cm 解析:①当弦 MN 和 EF 在圆心同侧时,如图
(1).
∵EF=16 cm,MN=12 cm,
∴CE=8 cm,MD=6 cm.
∵OE=OM=10 cm,
∴OC=6 cm,OD=8 cm.
∴CD=OD-OC=2 cm.

②当弦 MN 和 EF 在圆心异侧时,如图
(2).
由①知 OC=6 cm,OD=8 cm.
∴CD=OC+OD=14 cm.
2 cm 或 14 cm 解析:①当弦 MN 和 EF 在圆心同侧时,如图
(1).
∵EF=16 cm,MN=12 cm,
∴CE=8 cm,MD=6 cm.
∵OE=OM=10 cm,
∴OC=6 cm,OD=8 cm.
∴CD=OD-OC=2 cm.

②当弦 MN 和 EF 在圆心异侧时,如图
(2).
由①知 OC=6 cm,OD=8 cm.
∴CD=OC+OD=14 cm.
12. (14分)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面; (保留作图痕迹)
(2)若这个输水管道有水部分的水面宽$AB = 16$ cm,水最深地方的高度为4 cm,求这个圆形截面的半径.

(1)请你补全这个输水管道的圆形截面; (保留作图痕迹)
(2)若这个输水管道有水部分的水面宽$AB = 16$ cm,水最深地方的高度为4 cm,求这个圆形截面的半径.

答案:
(1)如图,先作弦 AB 的垂直平分线;在弧 AB 上任取一点 C,连接 AC,作弦 AC 的垂直平分线,两线交点作为圆心 O,OA 作为半径,画圆即为所求图形.

(2)如图,弦 AB 的垂直平分线交 AB 于点 D,交弧 AB 于点 E,连接 OB.
∵OE⊥AB,
∴BD=$\frac{1}{2}$AB=$\frac{1}{2}×16$=8(cm).
由题意可知,ED=4 cm.
设半径为 x cm,则 OD=(x-4)cm.
在 Rt△BOD 中,由勾股定理,得
OD²+BD²=OB²,
∴$(x-4)^2+8^2=x^2$,解得 x=10,
即这个圆形截面的半径为 10 cm.
(1)如图,先作弦 AB 的垂直平分线;在弧 AB 上任取一点 C,连接 AC,作弦 AC 的垂直平分线,两线交点作为圆心 O,OA 作为半径,画圆即为所求图形.

(2)如图,弦 AB 的垂直平分线交 AB 于点 D,交弧 AB 于点 E,连接 OB.
∵OE⊥AB,
∴BD=$\frac{1}{2}$AB=$\frac{1}{2}×16$=8(cm).
由题意可知,ED=4 cm.
设半径为 x cm,则 OD=(x-4)cm.
在 Rt△BOD 中,由勾股定理,得
OD²+BD²=OB²,
∴$(x-4)^2+8^2=x^2$,解得 x=10,
即这个圆形截面的半径为 10 cm.
查看更多完整答案,请扫码查看


