《2025年名师帮同步学案九年级数学全一册人教版》

1. 在$Rt△ABC$中,$∠C=90^{\circ }$,则下列等式成立的是 (B)
A. $sinA=\frac {AC}{AB}$
B. $sinA=\frac {BC}{AB}$
C. $sinA=\frac {AC}{BC}$
D. $sinA=\frac {BC}{AC}$

答案： 1.B

2. 在$Rt△ABC$中,$∠C=90^{\circ },AB=5,BC=3$,则$sinA$的值是 (C)
A. $\frac {4}{3}$
B. $\frac {3}{4}$
C. $\frac {3}{5}$
D. $\frac {4}{5}$

答案： 2.C

3. 在$Rt△ABC$中,$∠C=90^{\circ }$,若$△ABC$的三边都扩大5倍,则$sinA$的值 (D)
A. 放大5倍
B. 缩小5倍
C. 不能确定
D. 不变

答案： 3.D

4. 三角形在正方形网格纸中的位置如图所示,则$sinα$的值是 $\frac{3}{5}$.

答案： 4.$\frac{3}{5}$

5. 在$Rt△ABC$中,$∠C=90^{\circ },BC:AC=5:12$,则$sinA=$$\frac{5}{13}$.

答案： 5.$\frac{5}{13}$

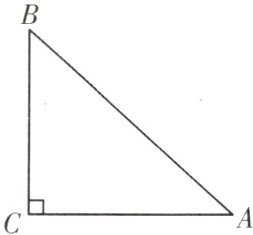
6. 如图,在$Rt△ABC$中,$∠C=90^{\circ },AC=12,sinB=\frac {3}{4}$,求 BC 的长和$sinA$的值.

答案： 解：$\because AC=12,\sin B=\frac{AC}{AB}=\frac{3}{4}$，
$\therefore AB=16$，
$\therefore BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{16^{2}-12^{2}}=4\sqrt{7}$，
$\therefore \sin A=\frac{BC}{AB}=\frac{4\sqrt{7}}{16}=\frac{\sqrt{7}}{4}$。

7. (循环练)一元二次方程$x^{2}-8x-2=0$配方后可变形为 (C)
A. $(x+4)^{2}=18$
B. $(x+4)^{2}=14$
C. $(x-4)^{2}=18$
D. $(x-4)^{2}=14$

答案： 7.C

8. 在$△ABC$中,$∠C=90^{\circ },sinA=\frac {2}{5}$,则$sinB$的值是 (D)
A. $\frac {2}{3}$
B. $\frac {2}{5}$
C. $\frac {4}{5}$
D. $\frac {\sqrt {21}}{5}$

答案： 8.D

9. 如图,点$A(t,4)$在第一象限,OA 与 x 轴所夹的锐角为$α,sinα=\frac {2}{3}$,则 t 的值为 $2\sqrt{5}$.

答案： 9.$2\sqrt{5}$

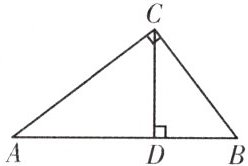
10. 如图,在$Rt△ABC$中,$∠ACB=90^{\circ },AB=5,BC=3,CD⊥AB$于点 D,求$sin∠BCD$的值.

答案： 解：$\because ∠ACB=90^{\circ }$，
$\therefore ∠B+∠A=90^{\circ }$，
$\because CD⊥AB$，
$\therefore ∠BDC=90^{\circ }$，
$\therefore ∠B+∠BCD=90^{\circ }$，
$\therefore ∠BCD=∠A$，
$\because AB=5,BC=3$，
$\therefore \sin ∠BCD=\sin A=\frac{BC}{AB}=\frac{3}{5}$。

11. 如图,点$D(0,3),O(0,0),C(4,0)$在$\odot A$上,BD 是$\odot A$的一条弦,则$sin∠OBD=$ (D)
A. $\frac {1}{2}$
B. $\frac {3}{4}$
C. $\frac {4}{5}$
D. $\frac {3}{5}$

答案： 11.D