《2025年名师帮同步学案九年级数学全一册人教版》

1.(2025·广州二中月考)下列事件中,是必然事件的是 (B)
A.任意买一张电影票,座位号是奇数
B.13个人中至少有两个人生相同
C.车辆随机到达一个路口,遇到绿灯
D.冬天的某一天一定会下雪

答案： B

2.下列说法正确的是 (A)
A.事件发生的可能性越大,它的概率越接近1
B.天气预报说每天下雨的概率是50%,所以明天将有一半的时间在下雨
C.彩票中奖的机会是1%,买100张一定会中奖
D.“从一个只有红球的袋子里摸出白球”是随机事件

答案： A

3.从2位男同学和2位女同学中任选2人参加志愿者活动,所选2人中恰好是一位男同学和一位女同学的概率是 (B)
A.$\frac {3}{4}$
B.$\frac {2}{3}$
C.$\frac {1}{2}$
D.$\frac {1}{4}$

答案： B

4.(2024·清城期末)在一个不透明的布袋中,红色、黄色、白色的玻璃球共有100个,除颜色外,形状、大小、质地等完全相同.小亮通过多次摸球试验后发现其中摸到红色、白色球的频率分别稳定在30%和45%,则布袋中黄色球的个数很可能是25个.

答案： 25

5.数学课上,李老师与学生们做“用频率估计概率”的试验:不透明袋子中有4个白球、3个红球、2个黄球和1个黑球,这些球除颜色外无其他差别.从袋子中随机取出一个球,某一颜色的球出现的频率如图所示,则该种球的颜色最有可能是 (C)

A.黑球
B.红球
C.黄球
D.白球

答案： C

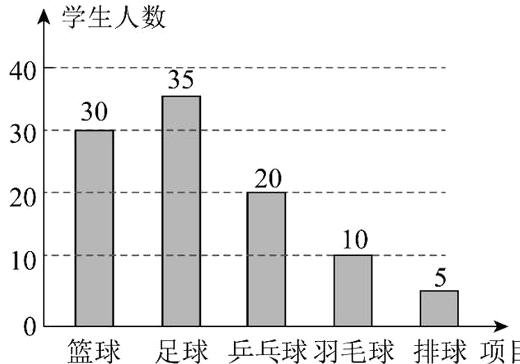
6.(2024·深圳期末)我校开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了一些学生(每名学生必选且只能选择这五项活动中的一种).根据以下统计图提供的信息,请解答下列问题:
(1)本次被调查的学生有____名,补全条形统计图;
(2)扇形统计图中“排球”对应的扇形的圆心角度数是____;
(3)学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛,请用列表法或面树状图法分析甲和乙同学同时被选中的概率.

答案：

(1)100 补全条形统计图如下:

(2)$18^{\circ }$
(3)解:画树状图如下:

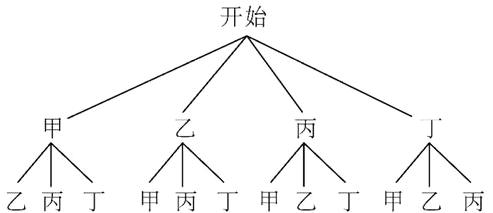
共有 12 种等可能的结果,其中甲和乙同学同时被选中的结果有 2 种,
$\therefore P$(甲和乙同学同时被选中)$=\frac {2}{12}=\frac {1}{6},$
∴甲和乙同学同时被选中的概率为$\frac {1}{6}.$