第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1.如图,已知直线$a// b// c$,直线$m$交直线$a$,$b$,$c$于点$A$,$B$,$C$,直线$n$交直线$a$,$b$,$c$于点$D$,$E$,$F$,若$\frac {AB}{BC}=\frac {1}{2}$,则$\frac {DE}{EF}=$(
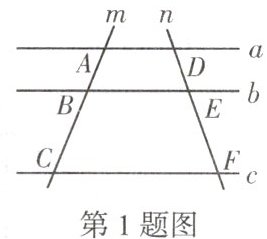
A.$\frac {1}{3}$
B.$\frac {1}{2}$
C.$\frac {2}{3}$
D.1
B
)
A.$\frac {1}{3}$
B.$\frac {1}{2}$
C.$\frac {2}{3}$
D.1
答案:
B
2.如图,已知点$D$为$\triangle ABC$边$AB$上的一点,$AD=2BD$,$DE// BC$交$AC$于$E$,$AE=6$,则$EC=$(
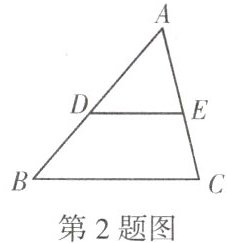
A.1
B.2
C.3
D.4
C
)
A.1
B.2
C.3
D.4
答案:
C
3.如图,$DE// BC$,$EF// AB$,则图中相似三角形一共有(
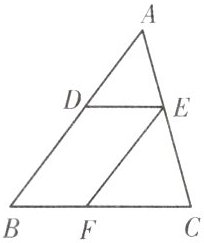
A.1对
B.2对
C.3对
D.4对
C
)
A.1对
B.2对
C.3对
D.4对
答案:
C
4.如图,$CD$与$BE$交于点$A$,$DE// BC$,$AE=3$,$AD=6$,$AC=8$.
(1)求证:$\triangle ABC\backsim \triangle AED$;
(2)求$AB$的长.

(1)求证:$\triangle ABC\backsim \triangle AED$;
(2)求$AB$的长.

答案:
(1) 证明:
∵ $ DE // BC $,
∴ $ \triangle ABC \backsim \triangle AED $;
(2) 解:
∵ $ \triangle ABC \backsim \triangle AED $,
∴ $ \frac{AE}{AB} = \frac{AD}{AC} $,
∴ $ \frac{3}{AB} = \frac{6}{8} $,
∴ $ AB = 4 $。
(1) 证明:
∵ $ DE // BC $,
∴ $ \triangle ABC \backsim \triangle AED $;
(2) 解:
∵ $ \triangle ABC \backsim \triangle AED $,
∴ $ \frac{AE}{AB} = \frac{AD}{AC} $,
∴ $ \frac{3}{AB} = \frac{6}{8} $,
∴ $ AB = 4 $。
5.如图,直线$AB$,$CD$,$EF$被直线$a$,$b$所截,若$∠1=100^{\circ }$,$∠2=100^{\circ }$,$∠3=125^{\circ }$,$∠4=55^{\circ }$,下列结论错误的是(
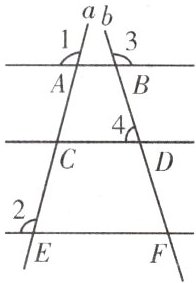
A.$EF// CD// AB$
B.$\frac {AC}{CE}=\frac {BD}{DF}$
C.$\frac {AB}{CD}=\frac {AC}{DF}$
D.$\frac {AC}{AE}=\frac {BD}{BF}$
C
)
A.$EF// CD// AB$
B.$\frac {AC}{CE}=\frac {BD}{DF}$
C.$\frac {AB}{CD}=\frac {AC}{DF}$
D.$\frac {AC}{AE}=\frac {BD}{BF}$
答案:
C
6.如图,在$□ ABCD$中,$EF// AB$,$DF:FB=2:3$.
(1)若$AE=6$,求$BC$的长;
(2)若$EF=4a$,则$CD=$____
(1)若$AE=6$,求$BC$的长;
(2)若$EF=4a$,则$CD=$____
10a
.
答案:
(1) 解:
∵ $ EF // AB $,
∴ $ \frac{DE}{AE} = \frac{DF}{FB} $,
∵ $ AE = 6 $,$ DF : FB = 2 : 3 $,
∴ $ \frac{DE}{6} = \frac{2}{3} $,
∴ $ DE = 4 $,
∴ $ AD = AE + DE = 6 + 4 = 10 $,
∵ 四边形 $ ABCD $ 是平行四边形,
∴ $ BC = AD = 10 $。
(2) $ 10a $ 解析:
∵ $ EF // AB $,
∴ $ \triangle DEF \backsim \triangle DAB $,
∴ $ \frac{EF}{AB} = \frac{DF}{DB} $,
∵ $ DF : FB = 2 : 3 $,
∴ $ DF : DB = 2 : 5 $,
∵ $ EF = 4a $,
∴ $ \frac{4a}{AB} = \frac{2}{5} $,
∴ $ AB = 10a $,
∵ 四边形 $ ABCD $ 是平行四边形,
∴ $ CD = AB = 10a $。
(1) 解:
∵ $ EF // AB $,
∴ $ \frac{DE}{AE} = \frac{DF}{FB} $,
∵ $ AE = 6 $,$ DF : FB = 2 : 3 $,
∴ $ \frac{DE}{6} = \frac{2}{3} $,
∴ $ DE = 4 $,
∴ $ AD = AE + DE = 6 + 4 = 10 $,
∵ 四边形 $ ABCD $ 是平行四边形,
∴ $ BC = AD = 10 $。
(2) $ 10a $ 解析:
∵ $ EF // AB $,
∴ $ \triangle DEF \backsim \triangle DAB $,
∴ $ \frac{EF}{AB} = \frac{DF}{DB} $,
∵ $ DF : FB = 2 : 3 $,
∴ $ DF : DB = 2 : 5 $,
∵ $ EF = 4a $,
∴ $ \frac{4a}{AB} = \frac{2}{5} $,
∴ $ AB = 10a $,
∵ 四边形 $ ABCD $ 是平行四边形,
∴ $ CD = AB = 10a $。
7.如图,$AB$为半圆$O$的直径,$C$为$BA$延长线上一点,$CD$切半圆$O$于点$D$,连接$OD$,作$BE⊥CD$于点$E$,交半圆$O$于点$F$.已知$CE=12$,$BE=9$.
(1)求证:$\triangle COD\backsim \triangle CBE$;
(2)求半圆$O$的半径$r$的长.

(1)求证:$\triangle COD\backsim \triangle CBE$;
(2)求半圆$O$的半径$r$的长.

答案:
(1) 证明:
∵ $ CD $ 切半圆 $ O $ 于点 $ D $,
∴ $ OD \perp CD $,
又
∵ $ BE \perp CE $,
∴ $ OD // BE $,
∴ $ \triangle COD \backsim \triangle CBE $;
(2) 解:在 $ \text{Rt} \triangle BCE $ 中,$ CE = 12 $,$ BE = 9 $,
∴ $ BC = \sqrt{CE^2 + BE^2} = \sqrt{12^2 + 9^2} = 15 $,
由
(1) 知 $ \triangle COD \backsim \triangle CBE $,
∴ $ \frac{OD}{BE} = \frac{OC}{BC} $,即 $ \frac{r}{9} = \frac{15 - r}{15} $,
解得 $ r = \frac{45}{8} $。
(1) 证明:
∵ $ CD $ 切半圆 $ O $ 于点 $ D $,
∴ $ OD \perp CD $,
又
∵ $ BE \perp CE $,
∴ $ OD // BE $,
∴ $ \triangle COD \backsim \triangle CBE $;
(2) 解:在 $ \text{Rt} \triangle BCE $ 中,$ CE = 12 $,$ BE = 9 $,
∴ $ BC = \sqrt{CE^2 + BE^2} = \sqrt{12^2 + 9^2} = 15 $,
由
(1) 知 $ \triangle COD \backsim \triangle CBE $,
∴ $ \frac{OD}{BE} = \frac{OC}{BC} $,即 $ \frac{r}{9} = \frac{15 - r}{15} $,
解得 $ r = \frac{45}{8} $。
查看更多完整答案,请扫码查看


