第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. 如图,$l_{1},l_{2},l_{3}$是一组平行线,直线AC,DF分别与这组平行线依次相交于点A,B,C和点D,E,F。若$\frac {AB}{BC}=\frac {2}{3}$,则$\frac {EF}{DF}$的值为(

A. $\frac {2}{5}$
B. $\frac {1}{2}$
C. $\frac {3}{5}$
D. $\frac {2}{3}$
C
)
A. $\frac {2}{5}$
B. $\frac {1}{2}$
C. $\frac {3}{5}$
D. $\frac {2}{3}$
答案:
C
2. (2024·揭西期末)如图,已知D是$\triangle ABC$的边AC上一点,根据下列条件,不能判定$\triangle CAB\backsim \triangle CBD$的是(
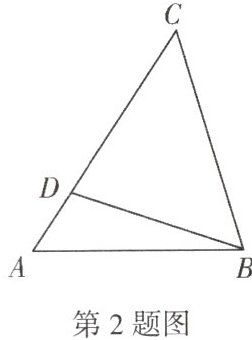
A. $∠A=∠CBD$
B. $∠CBA=∠CDB$
C. $AB\cdot CD=BD\cdot BC$
D. $BC^{2}=AC\cdot CD$
C
)
A. $∠A=∠CBD$
B. $∠CBA=∠CDB$
C. $AB\cdot CD=BD\cdot BC$
D. $BC^{2}=AC\cdot CD$
答案:
C 解析:
∵ $ ∠C $ 是公共角,
∴ 再加上 $ ∠A = ∠CBD $ 或 $ ∠CBA = ∠CDB $ 都可以证明 $ △CAB \backsim △CBD $,故选项 A,B 不符合题意;选项 C 中的两边成比例,但不是相应的夹角相等,
∴ 选项 C 符合题意。
∵ $ ∠C = ∠C $,若再添加 $ \frac{CD}{BC} = \frac{BC}{AC} $,即 $ BC^{2} = AC \cdot CD $,可证明 $ △CAB \backsim △CBD $,故选项 D 不符合题意。故选 C。
∵ $ ∠C $ 是公共角,
∴ 再加上 $ ∠A = ∠CBD $ 或 $ ∠CBA = ∠CDB $ 都可以证明 $ △CAB \backsim △CBD $,故选项 A,B 不符合题意;选项 C 中的两边成比例,但不是相应的夹角相等,
∴ 选项 C 符合题意。
∵ $ ∠C = ∠C $,若再添加 $ \frac{CD}{BC} = \frac{BC}{AC} $,即 $ BC^{2} = AC \cdot CD $,可证明 $ △CAB \backsim △CBD $,故选项 D 不符合题意。故选 C。
3. 在平面直角坐标系中,以原点O为位似中心,将$\triangle ABC$在第一象限内按相似比2放大后得到$\triangle A'B'C'$。若点A的坐标为$(2,3)$,则点$A'$的坐标为
$(4,6)$
。
答案:
$ (4,6) $
4. 如图,在$\triangle ABC$中,$DE// BC$,$EF// AB$。
(1) 求证:$\triangle ADE\backsim \triangle EFC$;
(2) 若$AE=2EC$,$DE=4$,求线段FC的长;
(3) 若$AE=2EC$,$S_{\triangle EFC}=4$时,四边形DEFB的面积是____
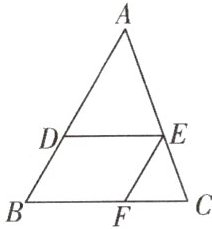
(1)
(2)
(1) 求证:$\triangle ADE\backsim \triangle EFC$;
(2) 若$AE=2EC$,$DE=4$,求线段FC的长;
(3) 若$AE=2EC$,$S_{\triangle EFC}=4$时,四边形DEFB的面积是____
16
。
(1)
证明:∵ $ DE // BC $,$ EF // AB $,
∴ $ ∠ADE = ∠B = ∠EFC $,$ ∠AED = ∠C $,
∴ $ △ADE \backsim △EFC $;
∴ $ ∠ADE = ∠B = ∠EFC $,$ ∠AED = ∠C $,
∴ $ △ADE \backsim △EFC $;
(2)
解:∵ $ △ADE \backsim △EFC $,
∴ $ \frac{AE}{EC} = \frac{DE}{FC} $,
∵ $ AE = 2EC $,$ DE = 4 $,
∴ $ 2 = \frac{4}{FC} $,
∴ $ FC = 2 $。
∴ $ \frac{AE}{EC} = \frac{DE}{FC} $,
∵ $ AE = 2EC $,$ DE = 4 $,
∴ $ 2 = \frac{4}{FC} $,
∴ $ FC = 2 $。
答案:
(1) 证明:
∵ $ DE // BC $,$ EF // AB $,
∴ $ ∠ADE = ∠B = ∠EFC $,$ ∠AED = ∠C $,
∴ $ △ADE \backsim △EFC $;
(2) 解:
∵ $ △ADE \backsim △EFC $,
∴ $ \frac{AE}{EC} = \frac{DE}{FC} $,
∵ $ AE = 2EC $,$ DE = 4 $,
∴ $ 2 = \frac{4}{FC} $,
∴ $ FC = 2 $。
(3) 16
(1) 证明:
∵ $ DE // BC $,$ EF // AB $,
∴ $ ∠ADE = ∠B = ∠EFC $,$ ∠AED = ∠C $,
∴ $ △ADE \backsim △EFC $;
(2) 解:
∵ $ △ADE \backsim △EFC $,
∴ $ \frac{AE}{EC} = \frac{DE}{FC} $,
∵ $ AE = 2EC $,$ DE = 4 $,
∴ $ 2 = \frac{4}{FC} $,
∴ $ FC = 2 $。
(3) 16
5. (2024·河源期末)如图,正方形ABCD的边长是3,$BP=CQ$,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①$AQ⊥DP$;②$OA^{2}=OD\cdot OP$;③$S_{\triangle AOD}=S_{四边OECF}$;④当$BP=1$时,$\frac {OE}{OA}=\frac {13}{16}$,正确结论的个数为( )
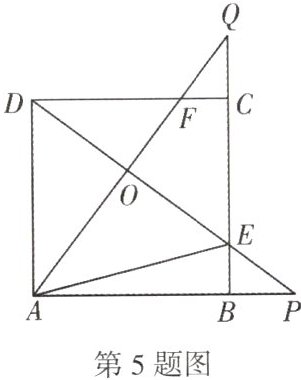
A. 1个
B. 2个
C. 3个
D. 4个
D

A. 1个
B. 2个
C. 3个
D. 4个
答案:
D 解析:
∵ 四边形 $ ABCD $ 是正方形,
∴ $ AD = BC $,$ ∠DAB = ∠ABC = 90^{\circ} $,
∵ $ BP = CQ $,
∴ $ AP = BQ $,在 $ △DAP $ 与 $ △ABQ $ 中,$ \begin{cases} AD = AB, \\ ∠DAP = ∠ABQ, \\ AP = BQ, \end{cases} $
∴ $ △DAP \cong △ABQ(SAS) $,
∴ $ ∠P = ∠Q $,
∵ $ ∠Q + ∠QAB = 90^{\circ} $,
∴ $ ∠P + ∠QAB = 90^{\circ} $,
∴ $ ∠AOP = 90^{\circ} $,
∴ $ AQ \perp DP $,故 ① 正确;
∵ $ ∠DOA = ∠AOP = 90^{\circ} $,$ ∠ADO + ∠P = ∠ADO + ∠DAO = 90^{\circ} $,
∴ $ ∠DAO = ∠P $,
∴ $ △DAO \backsim △APO $,
∴ $ \frac{AO}{DO} = \frac{OP}{OA} $,
∴ $ AO^{2} = OD \cdot OP $,故 ② 正确;在 $ △CQF $ 与 $ △BPE $ 中,$ \begin{cases} ∠FCQ = ∠EBP, \\ CQ = BP, \\ ∠Q = ∠P, \end{cases} $
∴ $ △CQF \cong △BPE(ASA) $,
∴ $ CF = BE $,
∴ $ DF = CE $,在 $ △ADF $ 与 $ △DCE $ 中,$ \begin{cases} AD = CD, \\ ∠ADC = ∠DCE, \\ DF = CE, \end{cases} $
∴ $ △ADF \cong △DCE(SAS) $,
∴ $ S_{△ADF} = S_{△DCE} $,
∴ $ S_{△ADF} - S_{△DFO} = S_{△DCE} - S_{△DOF} $,即 $ S_{△AOD} = S_{四边形OECF} $,故 ③ 正确;
∵ $ BP = 1 $,$ AB = 3 $,
∴ $ AP = 4 $,
∵ $ △PBE \backsim △PAD $,
∴ $ \frac{BP}{BE} = \frac{PA}{DA} = \frac{4}{3} $,
∴ $ BE = \frac{3}{4} $,
∴ $ QE = \frac{13}{4} $,
∵ $ △QOE \backsim △PAD $,
∴ $ \frac{OQ}{PA} = \frac{OE}{AD} = \frac{QE}{PD} = \frac{\frac{13}{4}}{5} = \frac{13}{20} $,
∴ $ OQ = \frac{13}{5} $,$ OE = \frac{39}{20} $,
∴ $ AO = 5 - OQ = \frac{12}{5} $,
∴ $ \frac{OE}{OA} = \frac{13}{16} $,故 ④ 正确。
故选 D。
∵ 四边形 $ ABCD $ 是正方形,
∴ $ AD = BC $,$ ∠DAB = ∠ABC = 90^{\circ} $,
∵ $ BP = CQ $,
∴ $ AP = BQ $,在 $ △DAP $ 与 $ △ABQ $ 中,$ \begin{cases} AD = AB, \\ ∠DAP = ∠ABQ, \\ AP = BQ, \end{cases} $
∴ $ △DAP \cong △ABQ(SAS) $,
∴ $ ∠P = ∠Q $,
∵ $ ∠Q + ∠QAB = 90^{\circ} $,
∴ $ ∠P + ∠QAB = 90^{\circ} $,
∴ $ ∠AOP = 90^{\circ} $,
∴ $ AQ \perp DP $,故 ① 正确;
∵ $ ∠DOA = ∠AOP = 90^{\circ} $,$ ∠ADO + ∠P = ∠ADO + ∠DAO = 90^{\circ} $,
∴ $ ∠DAO = ∠P $,
∴ $ △DAO \backsim △APO $,
∴ $ \frac{AO}{DO} = \frac{OP}{OA} $,
∴ $ AO^{2} = OD \cdot OP $,故 ② 正确;在 $ △CQF $ 与 $ △BPE $ 中,$ \begin{cases} ∠FCQ = ∠EBP, \\ CQ = BP, \\ ∠Q = ∠P, \end{cases} $
∴ $ △CQF \cong △BPE(ASA) $,
∴ $ CF = BE $,
∴ $ DF = CE $,在 $ △ADF $ 与 $ △DCE $ 中,$ \begin{cases} AD = CD, \\ ∠ADC = ∠DCE, \\ DF = CE, \end{cases} $
∴ $ △ADF \cong △DCE(SAS) $,
∴ $ S_{△ADF} = S_{△DCE} $,
∴ $ S_{△ADF} - S_{△DFO} = S_{△DCE} - S_{△DOF} $,即 $ S_{△AOD} = S_{四边形OECF} $,故 ③ 正确;
∵ $ BP = 1 $,$ AB = 3 $,
∴ $ AP = 4 $,
∵ $ △PBE \backsim △PAD $,
∴ $ \frac{BP}{BE} = \frac{PA}{DA} = \frac{4}{3} $,
∴ $ BE = \frac{3}{4} $,
∴ $ QE = \frac{13}{4} $,
∵ $ △QOE \backsim △PAD $,
∴ $ \frac{OQ}{PA} = \frac{OE}{AD} = \frac{QE}{PD} = \frac{\frac{13}{4}}{5} = \frac{13}{20} $,
∴ $ OQ = \frac{13}{5} $,$ OE = \frac{39}{20} $,
∴ $ AO = 5 - OQ = \frac{12}{5} $,
∴ $ \frac{OE}{OA} = \frac{13}{16} $,故 ④ 正确。
故选 D。
6. 如图,某测量工作人员的眼睛A与标杆顶端F,铁塔顶端E在一条直线上,已知此人眼睛距离地面的高为1.6m,标杆高为3.2m,且$BC=1m$,$CD=5m$,则铁塔的高$DE=$
11.2
m。
答案:
11.2
7. 如图,直线$y=kx+b$与反比例函数$y=\frac {6}{x}(x>0)$的图象分别交于点$A(m,3)$和点$B(6,n)$,与坐标轴分别交于点C和点D。
(1) 求直线AB的解析式;
(2) 若点P是x轴上一动点,当$\triangle COD$与$\triangle ADP$相似时,直接写出点P的坐标。
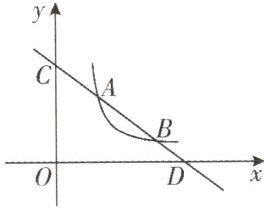
(1) 求直线AB的解析式;
(2) 若点P是x轴上一动点,当$\triangle COD$与$\triangle ADP$相似时,直接写出点P的坐标。

答案:
解:
(1)
∵ 点 $ A $,$ B $ 在 $ y = \frac{6}{x} $ 上,
∴ $ \frac{6}{m} = 3 $,$ \frac{6}{6} = n $,
∴ $ m = 2 $,$ n = 1 $,
∴ $ A $ 点坐标为 $ (2,3) $,$ B $ 点坐标为 $ (6,1) $,
则 $ \begin{cases} 2k + b = 3, \\ 6k + b = 1, \end{cases} $ 解得 $ \begin{cases} k = - \frac{1}{2}, \\ b = 4, \end{cases} $
∴ 直线 $ AB $ 的解析式为 $ y = - \frac{1}{2}x + 4 $;
(2)
∵ $ ∠ODC = ∠ADP $,
∴ $ △COD $ 与 $ △ADP $ 相似有 $ ∠PAD = ∠COD = 90^{\circ} $ 和 $ ∠APD = ∠COD = 90^{\circ} $ 两种情况。
① 如答图 1,当 $ ∠PAD = ∠COD = 90^{\circ} $ 时。

在 $ y = - \frac{1}{2}x + 4 $ 中,令 $ x = 0 $ 得 $ y = 4 $,令 $ y = 0 $ 得 $ x = 8 $,
∴ 点 $ C $ 坐标为 $ (0,4) $,点 $ D $ 坐标为 $ (8,0) $,
∴ $ OC = 4 $,$ OD = 8 $,$ AD = \sqrt{(8 - 2)^{2} + (0 - 3)^{2}} = 3\sqrt{5} $,
在 $ Rt△OCD $ 中,由勾股定理得 $ CD = \sqrt{4^{2} + 8^{2}} = 4\sqrt{5} $,
∵ $ △COD \backsim △PAD $,
∴ $ \frac{CD}{PD} = \frac{OD}{AD} $,即 $ \frac{4\sqrt{5}}{PD} = \frac{8}{3\sqrt{5}} $,
∴ $ PD = \frac{15}{2} $,
∴ $ OP = OD - PD = \frac{1}{2} $,
∴ 点 $ P $ 坐标为 $ (\frac{1}{2},0) $;
② 如答图 2,当 $ ∠APD = ∠COD = 90^{\circ} $ 时。

∵ $ AP \perp OD $,$ A(2,3) $,
∴ 点 $ P $ 坐标为 $ (2,0) $。
综上所述,当 $ △COD $ 与 $ △ADP $ 相似时,点 $ P $ 的坐标为 $ (\frac{1}{2},0) $ 或 $ (2,0) $。
解:
(1)
∵ 点 $ A $,$ B $ 在 $ y = \frac{6}{x} $ 上,
∴ $ \frac{6}{m} = 3 $,$ \frac{6}{6} = n $,
∴ $ m = 2 $,$ n = 1 $,
∴ $ A $ 点坐标为 $ (2,3) $,$ B $ 点坐标为 $ (6,1) $,
则 $ \begin{cases} 2k + b = 3, \\ 6k + b = 1, \end{cases} $ 解得 $ \begin{cases} k = - \frac{1}{2}, \\ b = 4, \end{cases} $
∴ 直线 $ AB $ 的解析式为 $ y = - \frac{1}{2}x + 4 $;
(2)
∵ $ ∠ODC = ∠ADP $,
∴ $ △COD $ 与 $ △ADP $ 相似有 $ ∠PAD = ∠COD = 90^{\circ} $ 和 $ ∠APD = ∠COD = 90^{\circ} $ 两种情况。
① 如答图 1,当 $ ∠PAD = ∠COD = 90^{\circ} $ 时。

在 $ y = - \frac{1}{2}x + 4 $ 中,令 $ x = 0 $ 得 $ y = 4 $,令 $ y = 0 $ 得 $ x = 8 $,
∴ 点 $ C $ 坐标为 $ (0,4) $,点 $ D $ 坐标为 $ (8,0) $,
∴ $ OC = 4 $,$ OD = 8 $,$ AD = \sqrt{(8 - 2)^{2} + (0 - 3)^{2}} = 3\sqrt{5} $,
在 $ Rt△OCD $ 中,由勾股定理得 $ CD = \sqrt{4^{2} + 8^{2}} = 4\sqrt{5} $,
∵ $ △COD \backsim △PAD $,
∴ $ \frac{CD}{PD} = \frac{OD}{AD} $,即 $ \frac{4\sqrt{5}}{PD} = \frac{8}{3\sqrt{5}} $,
∴ $ PD = \frac{15}{2} $,
∴ $ OP = OD - PD = \frac{1}{2} $,
∴ 点 $ P $ 坐标为 $ (\frac{1}{2},0) $;
② 如答图 2,当 $ ∠APD = ∠COD = 90^{\circ} $ 时。

∵ $ AP \perp OD $,$ A(2,3) $,
∴ 点 $ P $ 坐标为 $ (2,0) $。
综上所述,当 $ △COD $ 与 $ △ADP $ 相似时,点 $ P $ 的坐标为 $ (\frac{1}{2},0) $ 或 $ (2,0) $。
查看更多完整答案,请扫码查看


