《2025年名师帮同步学案九年级数学全一册人教版》

1. 视力表对我们来说并不陌生,如图,现需制作标准视力表,要求测试距离$l_{1}=5m$,此时字母E的高度为$b_{1}m$.由于场地有限,需要缩小测试距离为$l_{2}=3m$,修改后视力表字母E的高度为$b_{2}m$,则$b_{1}$与$b_{2}$的关系为 (D)
A. $\frac {b_{1}}{b_{2}}=\frac {5}{2}$
B. $\frac {b_{1}}{b_{2}}=\frac {8}{3}$
C. $\frac {b_{1}}{b_{2}}=\frac {8}{2}$
D. $\frac {b_{1}}{b_{2}}=\frac {5}{3}$

答案： 1.D

2. 如图,已知标杆$CD=3m$,标杆与旗杆AB的水平距离$BD=15m$,人的眼睛到地面的距离$EF=1.6m$,人与标杆CD的水平距离$DF=2m$,则旗杆AB的高度为13.5m.

答案： 2.13.5　解析:
∵CD⊥FB,AB⊥FB,
∴CD//AB,
∴△CGE∽△AHE,
∴$\frac{CG}{AH}$=$\frac{EG}{EH}$,即$\frac{CD−EF}{AH}$=$\frac{FD}{FD+BD}$,
∴$\frac{3−1.6}{AH}$=$\frac{2}{2+15}$,解得AH=11.9,
∴AB=AH+HB=AH+EF=11.9+1.6=13.5m.

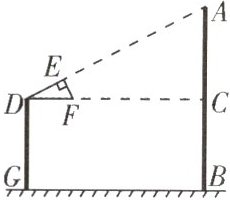
3. 如图,小明用直角三角板DEF测量树AB的高度,他调整自己的位置,设法使斜边DF保持水平,并且直角边DE与点A在同一直线上.已知$DE=0.4m,EF=0.2m$,边DF离地面的高度$DG=1.5m$,小明与树的距离$BG=8m$,求树AB的高度.

答案： 3.解:由题意，得四边形BCDG是矩形.
∴CB=DG=1.5m,CD=BG=8m,
∵∠DEF=∠DCA=90°,∠EDF=∠CDA,
∴△DEF∽△DCA,
∴$\frac{DE}{DC}$=$\frac{EF}{CA}$,即$\frac{0.4}{8}$=$\frac{0.2}{CA}$,
　解得CA=4,
∴AB=CB+CA=1.5+4=5.5m.
　答:树AB的高度为5.5m.

4. (循环练)如图,AB,AC,BD是$\odot O$的切线,切点分别是点P,C,D.若$AB=5,AC=3$,则BD的长是 (C)
A. 4
B. 3
C. 2
D. 1

答案： 4.C

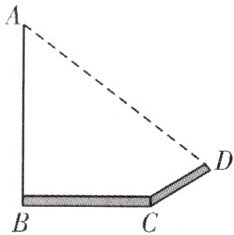
5. 如图,小莉发现垂直地面的电线杆AB的影子落在水平地面和土坡上,影长分别为BC和CD,测得$BC=20m,CD=8m$,CD与地面成$30^{\circ }$角,且此时测得垂直于地面的长为1m的标杆在地面上的影长为2m,求电线杆AB的长度.

答案：
5.解:如图，过点D作DE⊥AB于点E,过点D 作DF⊥BC交BC的延长线于点F.
　　　　　　
∵∠DCF=30°,
∴DF=$\frac{1}{2}$CD=4m,CF=$\sqrt{CD^2 - DF^2}$=4$\sqrt{3}$m,
∴DE=BF=BC+CF=(20+4$\sqrt{3}$)m.
∵垂直于地面的1m长标杆在地面上影长为2m,
∴AE=$\frac{1}{2}$DE=(10+2$\sqrt{3}$)m,
∴AB=AE+BE=AE+DF=10+2$\sqrt{3}$+4=(14+2$\sqrt{3}$)m.

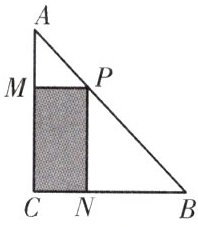
6. 如图,将直角三角形余料截出一个矩形PMCN,$∠C=90^{\circ },AC=8cm,BC=6cm$,点P,M,N分别在AB,AC,BC上,设$CN=xcm$.
(1)试用含x的代数式表示PN;
(2)设矩形PMCN的面积为$ycm^{2}$,当x为何值时,y的值最大?最大值是多少?

答案： 6.解:
(1)
∵CN=x,
∴BN=6−x,
∵△BNP∽△BCA,
∴$\frac{BN}{BC}$=$\frac{PN}{AC}$,
∴$\frac{6−x}{6}$=$\frac{PN}{8}$,
∴PN=8−$\frac{4}{3}$x;
(2)依题意得,y=CN·PN=x(8 - $\frac{4}{3}$x)=−$\frac{4}{3}$(x−3)²+12,
　当x=3时,y最大=12.

7. 如图,小明从路灯AB走向路灯CD时发现,当他走到点E时,头的顶部F的影子恰好与点A重合,当他向前走15m到达G点时,头的顶部H的影子恰好与点C重合,已知小明的身高是1.7m,两个路灯的高度都是8.5m,则$AC=$25m.

答案： 7.25　　解析:
∵EF//CD,
∴△AEF∽△ACD,
∴$\frac{EF}{CD}$=$\frac{AE}{AC}$,即$\frac{1.7}{8.5}$=$\frac{AE}{AE+15+CG}$,即AE+15+CG=5AE,
∵GH//AB,
∴△CGH∽△CAB,
∴$\frac{GH}{AB}$=$\frac{CG}{CA}$,$\frac{1.7}{8.5}$=$\frac{CG}{AE+15+CG}$,即AE+15+CG=5CG,
∴AE=CG=5,
∴AC=5+15+5=25m.