第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. 若关于x的一元二次方程$(k-1)x^{2}+4x+1=0$有两个不相等的实数根,则k的取值范围是(
A. $k<5$
B. $k>5$
C. $k>5$且$k≠1$
D. $k<5$且$k≠1$
D
)A. $k<5$
B. $k>5$
C. $k>5$且$k≠1$
D. $k<5$且$k≠1$
答案:
D
2. 把$x^{2}-5x=31$配方,需在方程的两边都加上(
A. 5
B. 25
C. 2.5
D. $\frac {25}{4}$
D
)A. 5
B. 25
C. 2.5
D. $\frac {25}{4}$
答案:
D
3. 关于x的一元二次方程$x^{2}+a^{2}-1=0$的一个根是$x=0$,则a的值为(
A. -1
B. 1
C. 1或-1
D. 3
C
)A. -1
B. 1
C. 1或-1
D. 3
答案:
C
4. 设α,β是方程$x^{2}+x-2025=0$的两个实数根,$α^{2}+2α+β$的值是
2024
.
答案:
2024
5. 解方程:
(1)$(2x+1)^{2}-4=0;$
(2)$x^{2}-4x-3=0;$
(3)$x(2x-5)=2(2x-5);$
(4)$3x^{2}-6x-2=0.$
(1)$(2x+1)^{2}-4=0;$
(2)$x^{2}-4x-3=0;$
(3)$x(2x-5)=2(2x-5);$
(4)$3x^{2}-6x-2=0.$
答案:
解:
(1)(2x + 1)² - 4 = 0
(2x + 1)² = 4
则 2x + 1 = 2 或 2x + 1 = -2,
解得 x₁ = $\frac{1}{2}$,x₂ = -$\frac{3}{2}$;
(2)x² - 4x = 3
则 x² - 4x + 4 = 3 + 4,即(x - 2)² = 7,
x - 2 = ±$\sqrt{7}$,
解得 x₁ = 2 + $\sqrt{7}$,x₂ = 2 - $\sqrt{7}$;
(3)x(2x - 5) = 2(2x - 5),
x(2x - 5) - 2(2x - 5) = 0,
(2x - 5)(x - 2) = 0,
解得 x₁ = $\frac{5}{2}$,x₂ = 2;
(4)
∵ a = 3,b = -6,c = -2,
∴ b² - 4ac = (-6)² - 4×3×(-2) = 60>0,
∴ x = $\frac{6 ± \sqrt{60}}{2×3}$ = $\frac{3 ± \sqrt{15}}{3}$,即 x₁ = $\frac{3 + \sqrt{15}}{3}$,x₂ = $\frac{3 - \sqrt{15}}{3}$。
(1)(2x + 1)² - 4 = 0
(2x + 1)² = 4
则 2x + 1 = 2 或 2x + 1 = -2,
解得 x₁ = $\frac{1}{2}$,x₂ = -$\frac{3}{2}$;
(2)x² - 4x = 3
则 x² - 4x + 4 = 3 + 4,即(x - 2)² = 7,
x - 2 = ±$\sqrt{7}$,
解得 x₁ = 2 + $\sqrt{7}$,x₂ = 2 - $\sqrt{7}$;
(3)x(2x - 5) = 2(2x - 5),
x(2x - 5) - 2(2x - 5) = 0,
(2x - 5)(x - 2) = 0,
解得 x₁ = $\frac{5}{2}$,x₂ = 2;
(4)
∵ a = 3,b = -6,c = -2,
∴ b² - 4ac = (-6)² - 4×3×(-2) = 60>0,
∴ x = $\frac{6 ± \sqrt{60}}{2×3}$ = $\frac{3 ± \sqrt{15}}{3}$,即 x₁ = $\frac{3 + \sqrt{15}}{3}$,x₂ = $\frac{3 - \sqrt{15}}{3}$。
6. 对于一元二次方程$ax^{2}+bx+c=0(a≠0)$,下列说法:
①若$a+b+c=0$,则$b^{2}-4ac=0;$
②若方程$ax^{2}+c=0$有两个不相等的实根,则方程$ax^{2}+bx+c=0$必有两个不相等的实根;
③若c是方程$ax^{2}+bx+c=0$的一个根,则一定有$ac+b+1=0$成立;
④若$x_{0}$是一元二次方程$ax^{2}+bx+c=0$的根,则$b^{2}-4ac=(2ax_{0}+b)^{2}.$
其中正确的是(
A. ①②④
B. ①②③
C. ①③④
D. ②③④
①若$a+b+c=0$,则$b^{2}-4ac=0;$
②若方程$ax^{2}+c=0$有两个不相等的实根,则方程$ax^{2}+bx+c=0$必有两个不相等的实根;
③若c是方程$ax^{2}+bx+c=0$的一个根,则一定有$ac+b+1=0$成立;
④若$x_{0}$是一元二次方程$ax^{2}+bx+c=0$的根,则$b^{2}-4ac=(2ax_{0}+b)^{2}.$
其中正确的是(
A
)A. ①②④
B. ①②③
C. ①③④
D. ②③④
答案:
A 解析:①当 x = 1 时,a×1² + b×1 + c = a + b + c = 0,那么一元二次方程 ax² + bx + c = 0(a≠0)有两个不相等的实数根或有两个相等的实数根,此时 b² - 4ac≥0 成立,那么①一定正确。②方程 ax² + c = 0 有两个不相等的实根,则 -4ac>0,那么 b² - 4ac>0,故方程 ax² + bx + c = 0 (a≠0)必有两个不相等的实根,进而推断出②正确。③由 c 是方程 ax² + bx + c = 0 的一个根,得 ac² + bc + c = 0。当 c≠0,则 ac + b + 1 = 0;当 c = 0,则 ac + b + 1 不一定等于 0,那么③不一定正确。④(2ax₀ + b)² = 4a²x₀² + b² + 4abx₀,由 b² - 4ac = 4a²x₀² + b² + 4abx₀,得 ax₀² + bx₀ + c = 0。由 x₀ 是一元二次方程 ax² + bx + c = 0 的根,则 ax₀² + bx₀ + c = 0 成立,那么④正确。
综上:正确的有①②④。故选 A。
综上:正确的有①②④。故选 A。
7. 如图,在矩形OABC纸片中,$OA=7,OC=5$,D为BC边上动点,将$△OCD$沿OD折叠,当点C的对应点落在直线AF上时,记为点E,若此时连接CE,同时$OA=OF$,则$△OCE$面积为____.


答案:
$\frac{15}{2}$ 或 10 解析:如图,作 EM⊥OF 于 M。设 EM = x。

∵ 四边形 OABC 是矩形,
∴ ∠AOC = 90°,
∵ OA = OF = 7,
∴ ∠F = ∠FAO = 45°,
∵ ∠FME = ∠FOA = 90°,
∴ ∠FEM = 45° = ∠F,
∴ ME = MF = x,OM = 7 - x,在 Rt△OEM 中,
∵ OM² + EM² = OE²,
∴ x² + (7 - x)² = 5²,解得 x = 3 或 4,
∴ S△COE = $\frac{1}{2}$×5×3 = $\frac{15}{2}$ 或 S△COE = $\frac{1}{2}$×5×4 = 10。
$\frac{15}{2}$ 或 10 解析:如图,作 EM⊥OF 于 M。设 EM = x。

∵ 四边形 OABC 是矩形,
∴ ∠AOC = 90°,
∵ OA = OF = 7,
∴ ∠F = ∠FAO = 45°,
∵ ∠FME = ∠FOA = 90°,
∴ ∠FEM = 45° = ∠F,
∴ ME = MF = x,OM = 7 - x,在 Rt△OEM 中,
∵ OM² + EM² = OE²,
∴ x² + (7 - x)² = 5²,解得 x = 3 或 4,
∴ S△COE = $\frac{1}{2}$×5×3 = $\frac{15}{2}$ 或 S△COE = $\frac{1}{2}$×5×4 = 10。
8. 某牧场准备利用现成的一堵“7”字形的墙面(粗线A-B-C表示墙面)建饲养场,已知$AB⊥BC,AB=3$米,$BC=15$米,现计划用总长为38米的篱笆围建一个“日”字形的饲养场BDEF,并在每个区域开一个宽2米的门,如图(细线表示篱笆,饲养场中间用篱笆GH隔开),点F可能在线段BC上,也可能在线段BC的延长线上.
(1)如图,当点F在线段BC上时,
①设EF的长为x米,则$DE=$
②若围成的饲养场BDEF的面积为132平方米,求饲养场的宽EF的长;
(2)如图当点F在线段BC延长线上,所围成的饲养场BDEF的面积能否为156平方米?如果能达到,求出EF的长;如果不能,请说明理由.

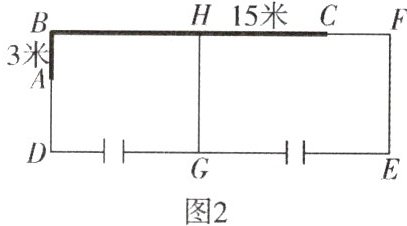
(1)如图,当点F在线段BC上时,
①设EF的长为x米,则$DE=$
(45 - 3x)
米;(用含x的代数式表示)②若围成的饲养场BDEF的面积为132平方米,求饲养场的宽EF的长;
解:(1)②依题意得 x(45 - 3x) = 132,
整理得 x² - 15x + 44 = 0,
解得 x₁ = 4,x₂ = 11。
当 x = 4 时,45 - 3x = 45 - 3×4 = 33>15,不合题意,舍去;
当 x = 11 时,45 - 3x = 45 - 3×11 = 12<15,符合题意。
答:饲养场的宽 EF 的长为 11 米;
整理得 x² - 15x + 44 = 0,
解得 x₁ = 4,x₂ = 11。
当 x = 4 时,45 - 3x = 45 - 3×4 = 33>15,不合题意,舍去;
当 x = 11 时,45 - 3x = 45 - 3×11 = 12<15,符合题意。
答:饲养场的宽 EF 的长为 11 米;
(2)如图当点F在线段BC延长线上,所围成的饲养场BDEF的面积能否为156平方米?如果能达到,求出EF的长;如果不能,请说明理由.
(2)不能达到,理由如下:
设 EF 的长为 y 米,则 DE = $\frac{38 + 15 + 2 + 2 - (3y - 3)}{2}$ = $\frac{60 - 3y}{2}$(米),
依题意得 y·$\frac{60 - 3y}{2}$ = 156,
整理得 y² - 20y + 104 = 0,
∵ Δ = (-20)² - 4×1×104 = -16<0,该方程没有实数根,
即当点 F 在线段 BC 延长线上,所围成的饲养场 BDEF 的面积不能达到 156 平方米。
设 EF 的长为 y 米,则 DE = $\frac{38 + 15 + 2 + 2 - (3y - 3)}{2}$ = $\frac{60 - 3y}{2}$(米),
依题意得 y·$\frac{60 - 3y}{2}$ = 156,
整理得 y² - 20y + 104 = 0,
∵ Δ = (-20)² - 4×1×104 = -16<0,该方程没有实数根,
即当点 F 在线段 BC 延长线上,所围成的饲养场 BDEF 的面积不能达到 156 平方米。


答案:
(1)①(45 - 3x)
解:
(1)②依题意得 x(45 - 3x) = 132,
整理得 x² - 15x + 44 = 0,
解得 x₁ = 4,x₂ = 11。
当 x = 4 时,45 - 3x = 45 - 3×4 = 33>15,不合题意,舍去;
当 x = 11 时,45 - 3x = 45 - 3×11 = 12<15,符合题意。
答:饲养场的宽 EF 的长为 11 米;
(2)不能达到,理由如下:
设 EF 的长为 y 米,则 DE = $\frac{38 + 15 + 2 + 2 - (3y - 3)}{2}$ = $\frac{60 - 3y}{2}$(米),
依题意得 y·$\frac{60 - 3y}{2}$ = 156,
整理得 y² - 20y + 104 = 0,
∵ Δ = (-20)² - 4×1×104 = -16<0,该方程没有实数根,
即当点 F 在线段 BC 延长线上,所围成的饲养场 BDEF 的面积不能达到 156 平方米。
(1)①(45 - 3x)
解:
(1)②依题意得 x(45 - 3x) = 132,
整理得 x² - 15x + 44 = 0,
解得 x₁ = 4,x₂ = 11。
当 x = 4 时,45 - 3x = 45 - 3×4 = 33>15,不合题意,舍去;
当 x = 11 时,45 - 3x = 45 - 3×11 = 12<15,符合题意。
答:饲养场的宽 EF 的长为 11 米;
(2)不能达到,理由如下:
设 EF 的长为 y 米,则 DE = $\frac{38 + 15 + 2 + 2 - (3y - 3)}{2}$ = $\frac{60 - 3y}{2}$(米),
依题意得 y·$\frac{60 - 3y}{2}$ = 156,
整理得 y² - 20y + 104 = 0,
∵ Δ = (-20)² - 4×1×104 = -16<0,该方程没有实数根,
即当点 F 在线段 BC 延长线上,所围成的饲养场 BDEF 的面积不能达到 156 平方米。
查看更多完整答案,请扫码查看


