第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. 司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数解析式是 (
A. $ v = \frac { 4 8 0 } { t } $
B. $ v + t = 4 8 0 $
C. $ v = \frac { 8 0 } { t } $
D. $ v = \frac { t - 6 } { t } $
A
)A. $ v = \frac { 4 8 0 } { t } $
B. $ v + t = 4 8 0 $
C. $ v = \frac { 8 0 } { t } $
D. $ v = \frac { t - 6 } { t } $
答案:
1. A
2. 如图所示是一个蓄水池每小时的排水量$ v m ^ { 3 } / h $与排完水池中的水所用时间$ t h $之间的函数关系图象,若要5h排完水池中的水,则每小时的排水量应为
$ 9.6 \, \text{m}^3/\text{h} $
.
答案:
2. $ 9.6 \, \text{m}^3/\text{h} $
3. 已知晋江市的耕地面积约为$ 3 7 5 k m ^ { 2 } $,人均占有的耕地面积S(单位:$ k m ^ { 2 } / $人)随全市人口n(单位:人)的变化而变化,则S与n的函数解析式是
$ S = \frac{375}{n} $
.
答案:
3. $ S = \frac{375}{n} $
4. 某养鱼专业户准备挖一个面积为$ 4 0 0 0 m ^ { 2 } $的长方形鱼塘.
(1)求鱼塘的长y(单位:m)关于宽x(单位:m)的函数解析式;
(2)由于受场地的限制,鱼塘的宽最多只能挖20m,则鱼塘的长至少为多少m?
(1)求鱼塘的长y(单位:m)关于宽x(单位:m)的函数解析式;
(2)由于受场地的限制,鱼塘的宽最多只能挖20m,则鱼塘的长至少为多少m?
答案:
4. 解:
(1)
∵ 长方形面积为 $ 4000 \, \text{m}^2 $,
∴ $ xy = 4000 $,即 $ y = \frac{4000}{x} (x > 0) $;
(2) 当 $ x = 20 $ 时,$ y = \frac{4000}{20} = 200 $,
∴ 鱼塘的长至少为 $ 200 \, \text{m} $。
(1)
∵ 长方形面积为 $ 4000 \, \text{m}^2 $,
∴ $ xy = 4000 $,即 $ y = \frac{4000}{x} (x > 0) $;
(2) 当 $ x = 20 $ 时,$ y = \frac{4000}{20} = 200 $,
∴ 鱼塘的长至少为 $ 200 \, \text{m} $。
5. 某品牌计算机春节期间搞活动,规定每台计算机售价0.7万元,首次付款后每个月应还的钱数y(单位:元)与还钱月数t的关系如图所示,其中y与t(单位:月)是反比例关系.
(1)根据图象写出y与t的函数解析式;
(2)求出首次付款的钱数;
(3)如果要求每月支付的钱数不多于400元,那么首付后还至少需几个月才能将所有的钱全部还清?

(1)根据图象写出y与t的函数解析式;
(2)求出首次付款的钱数;
(3)如果要求每月支付的钱数不多于400元,那么首付后还至少需几个月才能将所有的钱全部还清?

答案:
5. 解:
(1) 设函数的解析式是 $ y = \frac{k}{t} (k \neq 0) $,
把 $ (10, 600) $ 代入得 $ 600 = \frac{k}{10} $,解得 $ k = 6000 $,
则函数的解析式是 $ y = \frac{6000}{t} (t > 0) $;
(2)
∵ 每台计算机售价 $ 0.7 $ 万元 $ = 7000 $ 元,且以后需付款 $ 6000 $ 元,
∴ $ 7000 - 6000 = 1000 $ (元),
故首付的钱数为 $ 1000 $ 元;
(3) 由题意得 $ 400 \geq \frac{6000}{t} $,解得 $ t \geq 15 $,
则至少需 $ 15 $ 个月才能将所有的钱全部还清。
(1) 设函数的解析式是 $ y = \frac{k}{t} (k \neq 0) $,
把 $ (10, 600) $ 代入得 $ 600 = \frac{k}{10} $,解得 $ k = 6000 $,
则函数的解析式是 $ y = \frac{6000}{t} (t > 0) $;
(2)
∵ 每台计算机售价 $ 0.7 $ 万元 $ = 7000 $ 元,且以后需付款 $ 6000 $ 元,
∴ $ 7000 - 6000 = 1000 $ (元),
故首付的钱数为 $ 1000 $ 元;
(3) 由题意得 $ 400 \geq \frac{6000}{t} $,解得 $ t \geq 15 $,
则至少需 $ 15 $ 个月才能将所有的钱全部还清。
6. 如图,已知点A,B坐标分别为$ A ( 5,0 ) $,$ B ( 4,4 ) $,以OA,AB为边作平行四边形OABC,若一个反比例函数的图象经过C点.
(1)求点C的坐标;
(2)求这个反比例函数的解析式.
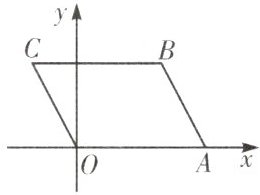
(1)求点C的坐标;
(2)求这个反比例函数的解析式.

答案:
6. 解:
(1)
∵ 四边形 $ OABC $ 为平行四边形,
设 $ BC $ 交 $ y $ 轴于点 $ E $,
∴ $ BC = AO = 5 $,$ BE = 4 $,$ EO = 4 $,
∴ $ EC = 1 $,
∴ 点 $ C $ 的坐标为 $ (-1, 4) $;
(2)
∵ 反比例函数的图象经过点 $ C $,
∴ 反比例函数的解析式为 $ y = -\frac{4}{x} $。
(1)
∵ 四边形 $ OABC $ 为平行四边形,
设 $ BC $ 交 $ y $ 轴于点 $ E $,
∴ $ BC = AO = 5 $,$ BE = 4 $,$ EO = 4 $,
∴ $ EC = 1 $,
∴ 点 $ C $ 的坐标为 $ (-1, 4) $;
(2)
∵ 反比例函数的图象经过点 $ C $,
∴ 反比例函数的解析式为 $ y = -\frac{4}{x} $。
查看更多完整答案,请扫码查看


