《2025年名师帮同步学案九年级数学全一册人教版》

1. 下列说法正确的是 (D)
A. 相等的圆心角所对的弧相等
B. 相等的弦所对的弧相等
C. 相等的圆周角所对的弧相等
D. 等弧所对的弦相等

答案： D

2. (2025·西藏一模)如图，AB是$\odot O$的直径，CD是$\odot O$的弦，$AB⊥CD$，垂足为E. 若$CD=8$，$OD=5$，则BE的长为 (B)

A. 1
B. 2
C. 3
D. 4

答案： B

3. 如图，AE为$\odot O$的直径，$\overset{\frown}{AB}=\overset{\frown}{BC}=\overset{\frown}{CD}$，$∠AOB=35^{\circ}$，则$∠DOE=$ (C)
A. $35^{\circ}$
B. $70^{\circ}$
C. $75^{\circ}$
D. $105^{\circ}$

答案： C

4. (2025·云浮期末)如图，四边形ABCD是$\odot O$的内接四边形. 若$∠A=45^{\circ}$，则$∠C$的度数为 (C)
A. $45^{\circ}$
B. $125^{\circ}$
C. $135^{\circ}$
D. $145^{\circ}$

答案： C

5. 已知圆锥的高是12，底面圆的半径为5，则这个圆锥的侧面展开图的周长为$26 + 10\pi$.

答案： $26 + 10\pi$

6. 如图，已知在$Rt△ABC$中，$∠B=90^{\circ}$，$AB=6$，$AC=10$，点P是$Rt△ABC$的内心. 点P到边AB的距离为2；

答案： 2

7. 如图，以等边$△ABC$的一边AB为直径的半圆O交AC于点D，交BC于点E，若$AB=4$，则阴影部分的面积是$\sqrt{3}$.

答案： $\sqrt{3}$

8. (2024·上海二模)我们把以三角形的重心为圆心的圆叫做该三角形的重心圆. 如图，在$△ABC$中，$AB=AC=10$，$BC=16$，如果$△ABC$的重心圆与该三角形各边的公共点一共有4个，那么它的半径R的取值范围是________________.

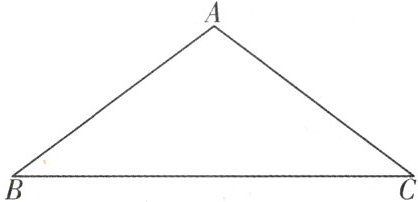
答案：
$R = 3.2$ 或 $4 ＜ R ＜ 2\sqrt{17}$ 解析：设点 $O$ 为 $\triangle ABC$ 的重心，

$\because AB = AC = 10$，$BC = 16$，$AD$ 为中线，
$\therefore AD \perp BC$，$\angle BAD = \angle CAD$，
$\therefore BD = CD = \frac{1}{2}BC = 8$，$AD = \sqrt{AC^2 - CD^2} =\sqrt{10^2 - 8^2} = 6$，
连接 $BO$，$CO$，则 $OD = 2$，$AO = 4$，
$\therefore BO = \sqrt{BD^2 + OD^2} = \sqrt{8^2 + 2^2} = 2\sqrt{17}$，
过点 $O$ 作 $OE \perp AC$ 于点 $E$，$OF \perp AB$ 于点 $F$，
$\therefore OE = OF$，
$\because S_{\triangle ABC} = \frac{1}{2}BC \cdot AD = \frac{1}{2} × 16 × 6 = 48$，
$S_{\triangle BOC} = \frac{1}{2}BC \cdot OD = \frac{1}{2} × 16 × 2 = 16$，
$\therefore S_{\triangle AOB} = S_{\triangle AOC} = \frac{1}{2}(48 - 16) = 16 = \frac{1}{2}AC \cdot OE$，
$\therefore$ 若 $\triangle ABC$ 的重心圆与该三角形各边的公共点一共有 4 个，那么它的半径 $R$ 的取值范围是 $R = 3.2$ 或 $4 ＜ R ＜ 2\sqrt{17}$。

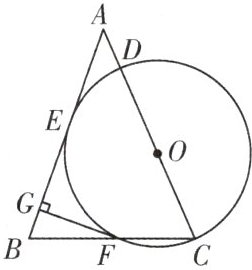
9. 如图，$△ABC$中，$AB=AC$，点D为AC上一点，以CD为直径的$\odot O$与AB相切于点E，交BC于点F，$FG⊥AB$，垂足为点G.
(1) 求证：FG是$\odot O$的切线；
(2) 若$\odot O$的半径为$2\sqrt{2}$，$BF=3$，求BE的长.

答案：

(1) 证明：如图，连接 $OF$。

$\because AB = AC$，$\therefore \angle B = \angle C$，
$\because OF = OC$，$\therefore \angle C = \angle OFC$，
$\therefore \angle OFC = \angle B$，$\therefore OF // AB$，
$\because FG \perp AB$，$\therefore FG \perp OF$，
又 $\because OF$ 是 $\odot O$ 半径，
$\therefore FG$ 是 $\odot O$ 的切线；
(2) 解：如图，连接 $OE$。
$\because \odot O$ 与 $AB$ 相切，$\therefore OE \perp AB$，
$\because AB \perp FG$，$OF \perp FG$，
$\therefore$ 四边形 $GFOE$ 是矩形，
$\therefore FG = OE = OF = EG = 2\sqrt{2}$，
在 $Rt\triangle BFG$ 中，由勾股定理，得
$BG = \sqrt{BF^2 - FG^2} = \sqrt{3^2 - (2\sqrt{2})^2} = 1$，
$\therefore BE = BG + EG = 1 + 2\sqrt{2}$。