第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1.随机掷一枚质地均匀的硬币两次,落地后至多有一次正面朝上的概率是 (
A.$\frac {3}{4}$
B.$\frac {2}{3}$
C.$\frac {1}{2}$
D.$\frac {1}{4}$
A
)A.$\frac {3}{4}$
B.$\frac {2}{3}$
C.$\frac {1}{2}$
D.$\frac {1}{4}$
答案:
1. A
2.取4张完全相同的卡片,分别写上A,B,C,D四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取1张,记下标号后放回.
(1)班长在4张卡片中随机抽到标号为C的概率为
(2)平平和安安两位同学抽到不同卡片的概率是多少?
(1)班长在4张卡片中随机抽到标号为C的概率为
$\frac{1}{4}$
;(2)平平和安安两位同学抽到不同卡片的概率是多少?
解: (2)列表如下,
| | A | B | C | D |
| --- | --- | --- | --- | --- |
| A | (A,A) | (B,A) | (C,A) | (D,A) |
| B | (A,B) | (B,B) | (C,B) | (D,B) |
| C | (A,C) | (B,C) | (C,C) | (D,C) |
| D | (A,D) | (B,D) | (C,D) | (D,D) |
一共有16种等可能的结果,其中抽到卡片不同的结果有12种,则平平和安安两位同学抽到不同卡片的概率是$\frac{12}{16}=\frac{3}{4}$.
| | A | B | C | D |
| --- | --- | --- | --- | --- |
| A | (A,A) | (B,A) | (C,A) | (D,A) |
| B | (A,B) | (B,B) | (C,B) | (D,B) |
| C | (A,C) | (B,C) | (C,C) | (D,C) |
| D | (A,D) | (B,D) | (C,D) | (D,D) |
一共有16种等可能的结果,其中抽到卡片不同的结果有12种,则平平和安安两位同学抽到不同卡片的概率是$\frac{12}{16}=\frac{3}{4}$.
答案:
2.
(1) $\frac{1}{4}$
解:
(2)列表如下,
| | A | B | C | D |
| --- | --- | --- | --- | --- |
| A | (A,A) | (B,A) | (C,A) | (D,A) |
| B | (A,B) | (B,B) | (C,B) | (D,B) |
| C | (A,C) | (B,C) | (C,C) | (D,C) |
| D | (A,D) | (B,D) | (C,D) | (D,D) |
一共有16种等可能的结果,其中抽到卡片不同的结果有12种,则平平和安安两位同学抽到不同卡片的概率是$\frac{12}{16}=\frac{3}{4}$.
(1) $\frac{1}{4}$
解:
(2)列表如下,
| | A | B | C | D |
| --- | --- | --- | --- | --- |
| A | (A,A) | (B,A) | (C,A) | (D,A) |
| B | (A,B) | (B,B) | (C,B) | (D,B) |
| C | (A,C) | (B,C) | (C,C) | (D,C) |
| D | (A,D) | (B,D) | (C,D) | (D,D) |
一共有16种等可能的结果,其中抽到卡片不同的结果有12种,则平平和安安两位同学抽到不同卡片的概率是$\frac{12}{16}=\frac{3}{4}$.
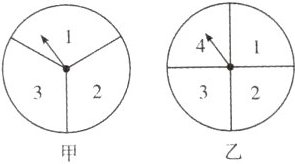
3.如图,甲、乙两个转盘分别被分成了3等份与4等份,每份内均标有数字,分别旋转这两个转盘,将转盘停止后指针所指区域内的两数相乘.
(1)求积为9的概率;
(2)求积为偶数的概率.
(1)求积为9的概率;
(2)求积为偶数的概率.

答案:
3. 解:所有结果列举如下,
(1)一共有12种等可能的情况,积为9的只有一种情况,
∴积为9的概率为$\frac{1}{12}$;
(2)一共有12种等可能的情况,积为偶数的有8种情况,
∴积为偶数的概率为$\frac{2}{3}$.
(1)一共有12种等可能的情况,积为9的只有一种情况,
∴积为9的概率为$\frac{1}{12}$;
(2)一共有12种等可能的情况,积为偶数的有8种情况,
∴积为偶数的概率为$\frac{2}{3}$.
4.(2024·廉江期末)(跨学科)如图,电路图上有1个小灯泡以及4个断开状态的开关A,B,C,D,现随机闭合两个开关,小灯泡发光的概率为 (
A.$\frac {1}{2}$
B.$\frac {1}{3}$
C.$\frac {2}{3}$
D.$\frac {3}{4}$
B
)A.$\frac {1}{2}$
B.$\frac {1}{3}$
C.$\frac {2}{3}$
D.$\frac {3}{4}$
答案:
4. B
5.从1,2,3,4四个数中随机选取两个不同的数,分别记为a,c,则关于x的一元二次方程$ax^{2}+4x+c=0$有实数根的概率为
A.$\frac {1}{4}$
B.$\frac {1}{3}$
C.$\frac {1}{2}$
D.$\frac {2}{3}$
C
A.$\frac {1}{4}$
B.$\frac {1}{3}$
C.$\frac {1}{2}$
D.$\frac {2}{3}$
答案:
5. C 解析:由一元二次方程$ax^{2}+4x+c=0$有实数根,得$\Delta =16-4ac$,即$ac\leqslant 4$,记为$(a,c)$.列表可得:
一共有12种等可能的结果,其中使$ac\leqslant 4$的有6种结果,
∴关于x的一元二次方程$ax^{2}+4x+c=0$有实数根的概率为$\frac{1}{2}$.故选C.
一共有12种等可能的结果,其中使$ac\leqslant 4$的有6种结果,
∴关于x的一元二次方程$ax^{2}+4x+c=0$有实数根的概率为$\frac{1}{2}$.故选C.
6.一个不透明的口袋中装有4个分别标有数字-3,-1,3,4的小球,它们的形状、大小完全相同,小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字4的小球的概率是
(2)请用列表法表示由x,y确定的点$P(x,y)$所有可能的结果;
解:列表如下:
|x\y|-3|-1|3|4|
|-3|—|(-3,-1)|(-3,3)|(-3,4)|
|-1|(-1,-3)|—|(-1,3)|(-1,4)|
|3|(3,-3)|(3,-1)|—|(3,4)|
|4|(4,-3)|(4,-1)|(4,3)|—|
共有12种等可能的结果;
(3)若规定:点$P(x,y)$在第一象限或第三象限小红获胜;点$P(x,y)$在第二象限或第四象限则小颖获胜,分别求出两人获胜的概率.
由(2)得,小红获胜的概率为$\frac{4}{12}=\frac{1}{3}$,
小颖获胜的概率为$\frac{8}{12}=\frac{2}{3}$.
(1)小红摸出标有数字4的小球的概率是
$\frac{1}{4}$
;(2)请用列表法表示由x,y确定的点$P(x,y)$所有可能的结果;
解:列表如下:
|x\y|-3|-1|3|4|
|-3|—|(-3,-1)|(-3,3)|(-3,4)|
|-1|(-1,-3)|—|(-1,3)|(-1,4)|
|3|(3,-3)|(3,-1)|—|(3,4)|
|4|(4,-3)|(4,-1)|(4,3)|—|
共有12种等可能的结果;
(3)若规定:点$P(x,y)$在第一象限或第三象限小红获胜;点$P(x,y)$在第二象限或第四象限则小颖获胜,分别求出两人获胜的概率.
由(2)得,小红获胜的概率为$\frac{4}{12}=\frac{1}{3}$,
小颖获胜的概率为$\frac{8}{12}=\frac{2}{3}$.
答案:
6.
(1) $\frac{1}{4}$
(2)解:列表如下:
共有12种等可能的结果;
(3)由
(2)得,小红获胜的概率为$\frac{4}{12}=\frac{1}{3}$,
小颖获胜的概率为$\frac{8}{12}=\frac{2}{3}$.
(1) $\frac{1}{4}$
(2)解:列表如下:
共有12种等可能的结果;
(3)由
(2)得,小红获胜的概率为$\frac{4}{12}=\frac{1}{3}$,
小颖获胜的概率为$\frac{8}{12}=\frac{2}{3}$.
查看更多完整答案,请扫码查看


