《2025年名师帮同步学案九年级数学全一册人教版》

1.如图,测得$BD=140m$,$DC=70m$,$EC=50m$,则河宽$AB$为 (B)
A.120m
B.100m
C.75m
D.25m

答案： B

2.如图,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6m的位置上,则球拍击球的高度$h$为 (C)
A.$\frac {8}{15}m$
B.1m
C.$\frac {4}{3}m$
D.$\frac {8}{5}m$

答案： C 解析：
∵ $ BC \perp AD $，$ DE \perp AD $，
∴ $ BC // DE $，
∴ $ \triangle ABC \backsim \triangle ADE $，$ \frac{0.8}{h} = \frac{6}{6 + 4} $，解得 $ h = \frac{4}{3} $。故选 C。

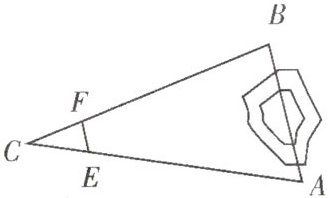
3.如图,$A$,$B$两点被池塘隔开,在$AB$外取一点$C$,连接$AC$,$BC$,在$AC$上取一点$E$,使$AE=3EC$,作$EF// AB$交$BC$于点$F$,量得$EF=6m$,则$AB$的长为______24 m.

答案： 24 m

4.如图是测量小玻璃管口径的量具$ABC$,$AB$的长为18cm,$AC$被分为60等份.如果小玻璃管口$DE$正好对着量具上20等份处($DE// AB$),那么小玻璃管口径$DE$长是______cm.

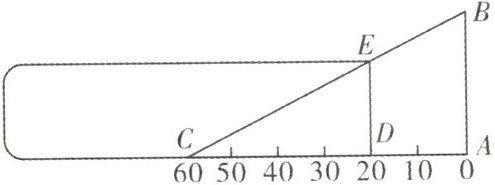
12

答案： 12

5.(循环练)一个不透明的袋子里装有质地、大小都相同的3个红球和1个绿球;随机从中摸出一球,不再放回,充分搅匀后再随机摸出一球,则两次摸到一红一绿的概率是 (C)
A.$\frac {1}{3}$
B.$\frac {2}{3}$
C.$\frac {1}{2}$
D.$\frac {1}{4}$

答案： C 解析：列表得，
∴ 一共有 12 种等可能的情况，其中两次摸到一红一绿的有 6 种情况，
∴ 两次摸到一红一绿的概率是 $ \frac{1}{2} $。故选 C。

6.(跨学科融合)如图是小明设计利用光线来测量某古城墙$CD$高度的示意图,如果镜子$P$与古城墙的距离$PD=12$米,镜子$P$与小明的距离$BP=1.5$米,小明刚好从镜子中看到古城墙顶端点$C$,小明眼睛距地面的高度$AB=1.2$米,那么该古城墙的高度是多少米?

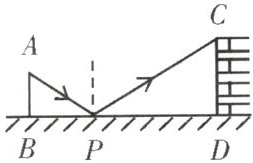
答案： 解：
∵ $ \angle APB = \angle CPD $，$ \angle ABP = \angle CDP $，
∴ $ \triangle ABP \backsim \triangle CDP $，
∴ $ \frac{AB}{CD} = \frac{BP}{PD} $，
即 $ \frac{1.2}{CD} = \frac{1.5}{12} $，
解得 $ CD = 9.6 $。
答：该古城墙的高度是 9.6 米。

7.如图,在一块斜边长30cm的直角三角形木板($Rt\triangle ACB$)上截取一个正方形$CDEF$,点$D$在边上$BC$,点$E$在斜边$AB$上,点$F$在边$AC$上,若$AF:AC=1:3$,则这块木板截取正方形$CDEF$后,剩余部分的面积为100$\text{cm}^2$.

答案： $ 100 \, \text{cm}^2 $ 解析：设 $ AF = x $，则 $ AC = 3x $，
∵ 四边形 $ CDEF $ 为正方形，
∴ $ EF = CF = 2x $，
$ EF // BC $，$ \triangle AEF \backsim \triangle ABC $，
∴ $ \frac{EF}{BC} = \frac{AF}{AC} = \frac{1}{3} $，
∴ $ BC = 6x $，在 $ \text{Rt} \triangle ABC $ 中，$ AB^2 = AC^2 + BC^2 $，即，$ 30^2 = (3x)^2 + (6x)^2 $，解得 $ x = 2\sqrt{5} $，
∴ $ AC = 6\sqrt{5} \, \text{cm} $，$ BC = 12\sqrt{5} \, \text{cm} $，
∴ 剩余部分的面积 $ = \frac{1}{2} × 12\sqrt{5} × 6\sqrt{5} - 4\sqrt{5} × 4\sqrt{5} = 100 \, \text{cm}^2 $。