《2025年名师帮同步学案九年级数学全一册人教版》

1.如图，$\odot O$是$\triangle ABC$的外接圆，$∠A=50^{\circ }$，则$∠BOC$的度数为（D）

A.$40^{\circ }$
B.$50^{\circ }$
C.$80^{\circ }$
D.$100^{\circ }$

答案： D

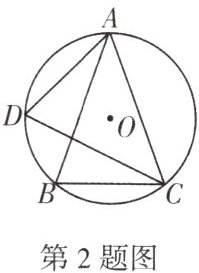
2.如图，在$\odot O$中，$\overset{\frown }{AB}=\overset{\frown }{AC}$，点D为$\odot O$上一点，若$∠D=70^{\circ }$，则$∠BAC=$（B）

A.$70^{\circ }$
B.$40^{\circ }$
C.$20^{\circ }$
D.$140^{\circ }$

答案： B

3.如图，AB是$\odot O$的直径，C，D为圆上两点，$∠AOC=130^{\circ }$，则$∠D$的度数为（A）

A.$25^{\circ }$
B.$30^{\circ }$
C.$35^{\circ }$
D.$50^{\circ }$

答案： A

4.如图，在$\odot O$中，弦BC与半径OA相交于点D.若$∠A=60^{\circ },∠ADC=88^{\circ }$，则$∠C=$$32^{\circ} $.

答案： $ 32^{\circ} $ 解析: $ \because \angle ADC = \angle A + \angle B $, $ \angle A = 60^{\circ} $, $ \angle ADC = 88^{\circ} $, $ \therefore \angle B = 28^{\circ} $, $ \therefore \angle AOC = 2\angle B = 56^{\circ} $, $ \because \angle ADC = \angle AOC + \angle C $, $ \therefore \angle C = 88^{\circ} - 56^{\circ} = 32^{\circ} $.

5.如图，$\odot O$的半径为4，点A，B，C在$\odot O$上，若$∠BAC=45^{\circ }$，则BC的长为$ 4\sqrt{2} $.

答案： $ 4\sqrt{2} $

6.如图，AB是$\odot O$的直径，CD是$\odot O$的弦，且$CD⊥AB$于点E.
（1）求证：$∠BCO=∠D$；
（2）若$\odot O$的半径为5，$AE=2$，求CD的长度.

答案：
(1)证明: $ \because OB = OC $,
$ \therefore \angle B = \angle OCB $.
$ \because \overset{\frown}{AC} = \overset{\frown}{AC} $,
$ \therefore \angle B = \angle D $,
$ \therefore \angle BCO = \angle D $;
(2)解: $ \because AB $ 是直径, $ AB \perp CD $,
$ \therefore CE = ED $,
$ \because OC = OA = 5 $, $ AE = 2 $,
$ \therefore OE = 3 $,
$ \because \angle CEO = 90^{\circ} $,
$ \therefore CE = \sqrt{CO^{2} - OE^{2}} = 4 $,
$ \therefore CD = 2CE = 8 $.

7.（2025·广州阶段练习）如图，CD是$\odot O$的直径，AB是$\odot O$的弦，$AB⊥CD$，垂足为点M，点E为$\overset{\frown }{AD}$上一点，且$\overset{\frown }{AE}=\overset{\frown }{AC}$，连接EC交AB于点F，连接AC.
（1）求证：$∠BAC=∠ECA$；
（2）若$OM=3,OC=5$，求AB的长.

答案：

(1)证明: $ \because CD $ 是 $ \odot O $ 的直径, $ AB $ 是 $ \odot O $ 的弦, $ AB \perp CD $,
$ \therefore \overset{\frown}{AC} = \overset{\frown}{BC} $,
又 $ \because \overset{\frown}{AE} = \overset{\frown}{AC} $,
$ \therefore \overset{\frown}{AE} = \overset{\frown}{BC} $,
$ \therefore \angle BAC = \angle ECA $;
(2)解:如图,连接 $ OA $.

$ \because OC = 5 $,
$ \therefore OA = OC = 5 $,
又 $ \because AB \perp CD $, $ OM = 3 $,
$ \therefore AM = \sqrt{OA^{2} - OM^{2}} = 4 $,
$ \because CD $ 是 $ \odot O $ 的直径, $ AB $ 是 $ \odot O $ 的弦, $ AB \perp CD $,
$ \therefore AB = 2AM = 8 $.