《2025年名师帮同步学案九年级数学全一册人教版》

1. 一个扇形的圆心角为$100^{\circ }$，半径长为$3\sqrt {6}cm$，求此扇形的面积。

答案： 解：
∵ $ n = 100 $，$ r = 3 \sqrt { 6 } \mathrm { cm } $，
∴ $ S = \frac { n \pi r ^ { 2 } } { 360 } = \frac { 100 \pi × ( 3 \sqrt { 6 } ) ^ { 2 } } { 360 } = 15 \pi \mathrm { cm } ^ { 2 } $．
∴ 此扇形的面积为 $ 15 \pi \mathrm { cm } ^ { 2 } $．

2. 半径为3cm，弧长为4cm的扇形面积为（C）
A. $4πcm^{2}$
B. $5cm^{2}$
C. $6cm^{2}$
D. $7πcm^{2}$

答案： C

3. 如图，点A，B，C在直径为$2\sqrt {3}$的$\odot O$上，$∠BAC=45^{\circ }$，则图中阴影部分的面积等于________（结果保留π）。

答案：
$ \frac { 3 } { 4 } \pi - \frac { 3 } { 2 } $ 解析：如图，连接 $ OB $，$ OC $，
∵ $ \angle B A C = 45 ^ { \circ } $，
∴ $ \angle B O C = 90 ^ { \circ } $，
∵ 圆的直径为 $ 2 \sqrt { 3 } $，
∴ $ OB = OC = \sqrt { 3 } $，
∴ $ S _ { \text { 扇形 } O B C } = \frac { 90 × \pi × ( \sqrt { 3 } ) ^ { 2 } } { 360 } = \frac { 3 } { 4 } \pi $，$ S _ { \triangle O B C } = \frac { 1 } { 2 } × \sqrt { 3 } × \sqrt { 3 } = \frac { 3 } { 2 } $，
∴ $ S _ { \text { 阴影 } } = S _ { \text { 扇形 } O B C } - S _ { \triangle O B C } = \frac { 3 } { 4 } \pi - \frac { 3 } { 2 } $．

4. 如图，CD为$\odot O$的弦，直径AB为4，$AB⊥CD$于点E，$∠A=30^{\circ }$，则扇形BOC的面积为（B）

A. $\frac {π}{3}$
B. $\frac {2π}{3}$
C. π
D. $\frac {4π}{3}$

答案： B

5. 已知圆心角为$60^{\circ }$的扇形面积为24π，那么该扇形的半径为（A）
A. 12
B. 6
C. $4π$
D. $2π$

答案： A

6. 某扇形的面积为6π，弧长为3π，此扇形的圆心角的度数为$135^{\circ}$。

答案： $ 135 ^ { \circ } $

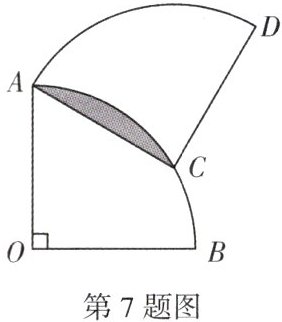
7. （2024·东莞期末）如图，扇形AOB的半径$OB=2$，将扇形AOB绕点A逆时针旋转得扇形ACD，当点C落在$\overset{\frown }{AB}$上时旋转停止，则扇形ACD中空白部分的面积为________（结果保留π）。

答案：
$ \frac { 1 } { 3 } \pi + \sqrt { 3 } $ 解析：连接 $ OC $，由旋转的性质得，$ A C = A O $，$ S _ { \text { 扇 } A C D } = S _ { \text { 扇 } A O B } $，扇形 $ A C D $ 中空白部分的面积 $ = $ 扇形 $ A O B $ 中空白部分的面积，
∵ $ O C = O A $，
∴ $ \triangle A O C $ 是等边三角形，
∴ $ \angle A O C = 60 ^ { \circ } $，
∴ $ \angle B O C = \angle A O B - \angle A O C = 90 ^ { \circ } - 60 ^ { \circ } = 30 ^ { \circ } $，
∵ $ O B = 2 $，
∴ $ S _ { \text { 扇 } B O C } = \frac { 30 \pi × 2 ^ { 2 } } { 360 } = \frac { 1 } { 3 } \pi $，过点 $ O $ 作 $ O H \perp A C $ 于点 $ H $，则 $ C H = \frac { 1 } { 2 } A C = 1 $，
∴ $ O H = \sqrt { O C ^ { 2 } - C H ^ { 2 } } = \sqrt { 2 ^ { 2 } - 1 ^ { 2 } } = \sqrt { 3 } $，
∴ $ S _ { \triangle A O C } = \frac { 1 } { 2 } × 2 × \sqrt { 3 } = \sqrt { 3 } $，
∴ 扇形 $ A O B $ 空白部分的面积 $ = S _ { \text { 扇 } B O C } + S _ { \triangle A O C } = \frac { 1 } { 3 } \pi + \sqrt { 3 } $．

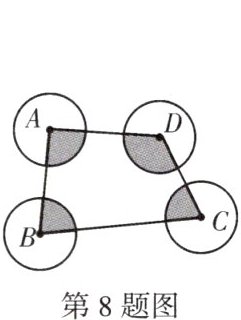
8. 如图，$\odot A,\odot B,\odot C,\odot D$的半径都为1，各圆互不相交。
（1）图中阴影部分（4个扇形）的面积的和为$\pi$；
（2）图中阴影部分（4个扇形）的弧长的和为$2\pi$。

答案：
(1) $ \pi $
(2) $ 2 \pi $

9. 如图，在$\odot O$中，弦BC垂直于半径OA，垂足为点E，点D是优弧$\overset{\frown }{BC}$上一点，连接BD，AD，OC，$∠ADB=30^{\circ }$。
（1）求$∠AOC$的度数；
（2）若弦$BC=6cm$，求阴影部分的面积。

答案：
解：
(1) 如图，连接 $ OB $．

∵ $ BC \perp OA $，
∴ $ BE = CE $，$ \overarc { AB } = \overarc { AC } $，
又
∵ $ \angle ADB = 30 ^ { \circ } $，
∴ $ \angle AOC = \angle AOB = 2 \angle ADB = 60 ^ { \circ } $；
(2)
∵ $ BC = 6 \mathrm { cm } $，
∴ $ CE = \frac { 1 } { 2 } BC = 3 \mathrm { cm } $．
由
(1) 知 $ \angle AOC = 60 ^ { \circ } $，
∴ $ \angle OCE = 30 ^ { \circ } $，
∴ $ OC = 2OE $，由勾股定理，得 $ OC ^ { 2 } = OE ^ { 2 } + CE ^ { 2 } $，即 $ ( 2OE ) ^ { 2 } = OE ^ { 2 } + 9 $，解得 $ OE = \sqrt { 3 } $，
∴ $ OC = 2 \sqrt { 3 } \mathrm { cm } $．
∵ $ \overarc { AB } = \overarc { AC } $，
∴ $ \angle BOC = 2 \angle AOC = 120 ^ { \circ } $，
∴ $ S _ { \text { 阴影 } } = S _ { \text { 扇形 } OBC } - S _ { \triangle OBC } = \frac { 120 } { 360 } × \pi × ( 2 \sqrt { 3 } ) ^ { 2 } - \frac { 1 } { 2 } × 6 × \sqrt { 3 } = ( 4 \pi - 3 \sqrt { 3 } ) \mathrm { cm } ^ { 2 } $．