《2025年名师帮同步学案九年级数学全一册人教版》

1.矩形的周长为12cm，设其一边长为xcm，面积为ycm²，则y与x之间的函数解析式及自变量x的取值范围均正确的是 (B)
A.$y=-x^{2}+6x(3＜x＜6)$
B.$y=-x^{2}+6x(0＜x＜6)$
C.$y=-x^{2}+12x(6＜x＜12)$
D.$y=-x^{2}+12x(0＜x＜12)$

答案： B

2.一个直角三角形的两条直角边的和为8cm，若它的一条直角边为xcm，面积为ycm².
(1)y与x之间的函数解析式为$ y = \frac{1}{2}x(8 - x) $；
(2)自变量x的取值范围是$ 0 ＜ x ＜ 8 $；
(3)当x为何值时，这个直角三角形的面积y最大？最大面积为多少？
解：$\because y = \frac{1}{2}x(8 - x) = -\frac{1}{2}(x - 4)^2 + 8$，
$\therefore$ 当 $ x = 4 \, \text{cm} $ 时，直角三角形的面积 $ y $ 最大，最大面积为 $ 8 \, \text{cm}^2 $。

答案：
(1) $ y = \frac{1}{2}x(8 - x) $
(2) $ 0 ＜ x ＜ 8 $
(3) 解：$\because y = \frac{1}{2}x(8 - x) = -\frac{1}{2}(x - 4)^2 + 8$，
$\therefore$ 当 $ x = 4 \, \text{cm} $ 时，直角三角形的面积 $ y $ 最大，最大面积为 $ 8 \, \text{cm}^2 $。

3.如图，用30m长的篱笆沿墙建造一边靠墙的矩形菜园，已知墙长18m，设矩形的宽AB为x m.
(1)用含x的代数式表示矩形的长BC；
(2)设矩形的面积为y m²，用含x的代数式表示矩形的面积y，并求出自变量的取值范围；
(3)这个矩形菜园的长和宽各为多少时，菜园的面积y最大？最大面积是多少？

答案： 解：
(1) $\because AB = CD = x \, \text{m}$，
$\therefore BC = (30 - 2x) \, \text{m}$；
(2) 由题意得 $ y = x(30 - 2x) = -2x^2 + 30x(6 \leq x ＜ 15) $；
(3) $\because y = -2x^2 + 30x = -2(x - 7.5)^2 + 112.5$，
$\therefore$ 当 $ x = 7.5 $ 时，$ y $ 有最大值，$ y_{\text{最大}} = 112.5 $，
$\therefore 30 - 2x = 30 - 2 × 7.5 = 15$，
$\therefore$ 这个矩形的长为 $ 15 \, \text{m} $、宽为 $ 7.5 \, \text{m} $ 时，菜园面积最大，最大面积为 $ 112.5 \, \text{m}^2 $。

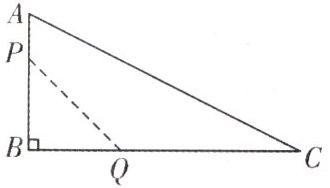
4.如图，在△ABC中，∠B=90°，AB=12m，BC=24m.动点P从点A开始沿边AB向点B以2m/s的速度运动(不与点B重合)，动点Q从点B开始沿边BC向点C以4m/s的速度运动(不与点C重合).如果点P，Q分别从点A，B同时出发，设运动时间为x s，四边形APQC的面积为y m².
(1)求y与x之间的函数关系式，直接写出自变量x的取值范围；
(2)经过多少秒时，四边形APQC的面积最小？最小值是多少？

答案： 解：
(1) 由题意，得 $ PB = (12 - 2x) \, \text{m} $，$ BQ = 4x \, \text{m} $。
$\therefore y = \frac{1}{2} × 12 × 24 - \frac{1}{2}(12 - 2x) \cdot 4x = 4x^2 - 24x + 144(0 ＜ x ＜ 6) $。
(2) $ y = 4x^2 - 24x + 144 = 4(x - 3)^2 + 108 $，
$\because 4 ＞ 0$，$ 0 ＜ x ＜ 6 $，
$\therefore$ 当 $ x = 3 $ 时，$ y $ 有最小值，最小值为 $ 108 $。
答：经过 $ 3 \, \text{s} $ 时，四边形 $ APQC $ 的面积最小，最小为 $ 108 \, \text{m}^2 $。