《2025年名师帮同步学案九年级数学全一册人教版》

1. 抛物线$y = - 2025x^{2}$的开口方向是（A）
A. 向下
B. 向上
C. 向左
D. 向右

答案： A

2. 二次函数$y = \frac{1}{2}x^{2}$的对称轴是（C）
A. 直线$y = 1$
B. 直线$x = 1$
C. $y$轴
D. $x$轴

答案： C

3. 二次函数$y = \frac{1}{3}x^{2}$的图象是抛物线，开口向上；对称轴是y轴，顶点坐标为(0, 0)；当x ＞ 0时，$y$随$x$的增大而增大，当x ＜ 0时，$y$随$x$的增大而减小；当x = 0时，$y$有最小值为0。

答案： 抛物线 向上 y轴 (0, 0) x ＞ 0 x ＜ 0 x = 0 小 0

4. 抛物线$y = 3x^{2}$，$y = - 3x^{2}$，$y = \frac{1}{3}x^{2}$共有的性质是（B）
A. 开口向下
B. 对称轴是$y$轴
C. 都有最高点
D. $y$随$x$的增大而增大

答案： B

5. 抛物线$y = - \frac{1}{2025}x^{2}$上有两点$(x_{1},y_{1})$，$(x_{2},y_{2})$，当$x_{1} \lt x_{2} \lt 0$时，$y_{1}$与$y_{2}$的大小关系为y₁ ＜ y₂。

答案： y₁ ＜ y₂

6.（循环练）解方程：$2000(1 + x)^{2} = 3380$。

答案： 解：二次项系数化为1，得 (1 + x)² = 1.69，由此可得 1 + x = ±1.3，即 x₁ = 0.3，x₂ = -2.3。

7.（循环练）如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，设$AB = x$米，则可列方程为x(100 - 4x) = 400。

答案： x(100 - 4x) = 400

8. 二次函数$y = kx^{2}$与一次函数$y = kx + k$在同一坐标系中的大致图象可能是（D）

答案： D

9. 抛物线$y = ax^{2}$与直线$y = - 2x - 4$交于点$(2,m)$。
（1）求$a$和$m$的值；
（2）写出抛物线的顶点坐标和对称轴；
（3）对于抛物线$y = ax^{2}$，当$x$取何值时，$y$随$x$的增大而增大？

答案： 解：
(1) 将 (2, m) 代入 y = -2x - 4，得 m = -4 - 4 = -8；将 (2, -8) 代入 y = ax²，得 4a = -8，解得 a = -2；
(2) 抛物线 y = -2x² 的顶点坐标为 (0, 0)，对称轴为 y 轴；
(3) 当 x ＜ 0 时，y 随 x 的增大而增大。

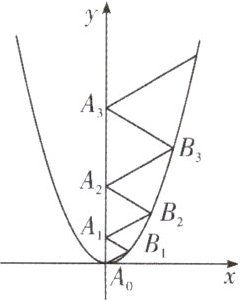
10. 二次函数$y = \frac{2}{3}x^{2}$的图象如图所示，点$A_{0}$位于坐标原点，点$A_{1}$，$A_{2}$，$A_{3}$，$\cdots$，$A_{2025}$在$y$轴的正半轴上，点$B_{1}$，$B_{2}$，$B_{3}$，$\cdots$，$B_{2025}$在二次函数$y = \frac{2}{3}x^{2}$位于第一象限的图象上，若$\triangle A_{0}B_{1}A_{1}$，$\triangle A_{1}B_{2}A_{2}$，$\triangle A_{2}B_{3}A_{3}$，$\cdots$，$\triangle A_{2024}B_{2025}A_{2025}$都为等边三角形，则$\triangle A_{2024}B_{2025}A_{2025}$的周长为____。

答案：
6075 解析：分别过 B₁，B₂，B₃ 作 y 轴的垂线，垂足分别为 A，B，C，

设 A₀A₁ = a，A₁A₂ = b，A₂A₃ = c，则 AB₁ = $\frac{\sqrt{3}}{2}a$，BB₂ = $\frac{\sqrt{3}}{2}b$，CB₃ = $\frac{\sqrt{3}}{2}c$，在等边 △A₀B₁A₁ 中，B₁($\frac{\sqrt{3}}{2}a$,$\frac{a}{2}$)，代入 y = $\frac{2}{3}x²$ 中，得 $\frac{a}{2}$ = $\frac{2}{3}$×$\frac{3}{4}a²$，解得 a = 1，即 A₀A₁ = 1，在等边 △A₁B₂A₂ 中，B₂($\frac{\sqrt{3}}{2}b$,$1 + \frac{b}{2}$)，代入 y = $\frac{2}{3}x²$ 中，得 $1 + \frac{b}{2}$ = $\frac{2}{3}$×$\frac{3}{4}b²$，解得 b = 2，即 A₁A₂ = 2，在等边 △A₂B₃A₃ 中，B₃($\frac{\sqrt{3}}{2}c$,$3 + \frac{c}{2}$)，代入 y = $\frac{2}{3}x²$ 中，得 $3 + \frac{c}{2}$ = $\frac{2}{3}$×$\frac{3}{4}c²$，解得 c = 3，即 A₂A₃ = 3，…以此类推由此可得 △A₂₀₂₄B₂₀₂₅A₂₀₂₅ 的边长为 2025，
∴△A₂₀₂₄B₂₀₂₅A₂₀₂₅ 的周长 = 2025×3 = 6075。