《2025年名师帮同步学案九年级数学全一册人教版》

1.如图，A，B是$\odot O$上的两点，AC是$\odot O$的切线，$∠B=65^{\circ }$，则$∠BAC=$（B）

A.$35^{\circ }$
B.$25^{\circ }$
C.$50^{\circ }$
D.$65^{\circ }$

答案： B

2.如图，已知BA是$\odot O$的切线，切点为点A，连接OB交$\odot O$于点C.若$∠B=45^{\circ },AB=2$，则BC的长为（）

A.$2\sqrt {2}-1$
B.$\sqrt {2}$
C.$2\sqrt {2}-2$
D.$2-\sqrt {2}$

答案：
C 解析:如图，连接OA,
∵BA是⊙O的切线，切点为点A,
∴∠OAB=90°,
∵∠B=45°,
∴△OAB是等腰直角三角形,
∵AB长为2,
∴AO=2,则BO=2√2,故BC=2√2−2.故选C.
　　　　　

3.（循环练）抛物线$y=-x^{2}+3x-1$与坐标轴的交点个数为（D）
A.0
B.1
C.2
D.3

答案： D

4.如图，$\odot O$的直径$AB=6cm$，D为$\odot O$上一点，过点D的切线交AB的延长线于点C，$AD=CD$，求：
（1）$∠A$的度数；
（2）CD的长.

答案：
解:
(1)如图，连接OD.
　　　　　
∵CD是⊙O的切线,
∴∠ODC=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD=CD,
∴∠C=∠CAD,
∴∠C=∠CAD=∠ODA,
　又
∵∠COD是△AOD的外角,
∴∠COD=∠OAD+∠ADO=2∠CAD,
　又
∵∠ODC=90°,
∴∠C+∠COD=90°,3∠CAD=90°,
∴∠CAD=30°,即∠A的度数为30°;
(2)
∵∠CAD=30°,
∴∠C=∠CAD=30°,
∵AB=6cm,
∴$OD= \frac { 1 } { 2 } AB = 3cm,　$在Rt△OCD中,∠ODC=90°,∠C=30°,
∴OC=2OD=6cm,
　根据勾股定理得CD=√(OC²−OD²)=√(36−9)=3√3cm,即CD的长为3√3cm.

5.如图，AB是$\odot O$的直径，直线CD与$\odot O$相切于点C，且与AB的延长线交于点E，点C是$\widehat {BF}$的中点，求证：$AD⊥CD.$

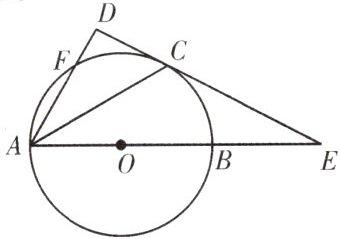
答案：
证明:如图，连接OC.
　　　　　
∵直线CD与⊙O相切,
∴OC⊥CD,
∵点C是$ \overarc { BF } $的中点,
∴∠DAC=∠EAC,
∵OA=OC,
∴∠OCA=∠EAC,
∴∠DAC=∠OCA,
∴OC//AD,
∴AD⊥CD.

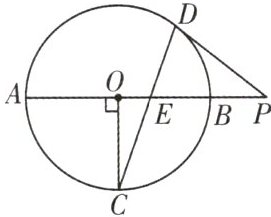
6.如图，AB为$\odot O$的直径，点C，D为$\odot O$上两点，连接OC，CD，CD交AB于点E，且$OC⊥AB$，过点D作$\odot O$的切线DP，交AB的延长线于点P.
（1）求证：$PD=PE;$
（2）若$\odot O$的半径为3，$BE=BP$，求CE的长.

答案：

(1)证明:如图，连接OD.
　　　　　
∵DP为⊙O的切线,
∴∠ODP=90°,即∠ODC+∠PDE=90°,
∵OC⊥AB,
∴∠OCD+∠OEC=90°,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠PDE=∠OEC,
　又
∵∠OEC=∠PED,
∴∠PDE=∠PED,
∴PD=PE;
(2)解:
∵⊙O的半径为3,
∴OC=OB=OD=3,
　设BE=BP=x,则PD=PE=BE+BP=2x,OP=3+x.
　在Rt△ODP中,由勾股定理,得OD²+PD²=OP²,
　即3²+(2x)²=(3+x)²,
　解得x₁=0(舍去),x₂=2,
∴BE=2,
∴OE=OB−BE=3−2=1,
　在Rt△OCE中,CE=√(OC²+OE²)=√(3²+1²)=√10