《2025年名师帮同步学案九年级数学全一册人教版》

1. 两个多边形相似的条件是 (D)
A. 对应角相等
B. 对应边成比例
C. 对应角相等或对应边成比例
D. 对应角相等且对应边成比例

答案： D

2. 如图所示的两个四边形相似, 则α的度数是 (C)
A. $60^{\circ}$
B. $75^{\circ}$
C. $87^{\circ}$
D. $120^{\circ}$

答案： C

3. 两个相似三角形的一组对应边的长分别为4.5 cm,3 cm, 则它们的相似比是 (A)
A. $\frac{3}{2}$
B. $\frac{4}{9}$
C. $\frac{2}{3}$
D. $\frac{9}{4}$

答案： A

4. 如图, $\triangle ABC$ 与 $\triangle DEF$ 相似, 相似比为 $\frac{1}{2}$,BC 的对应边是 EF, 若 $BC = 2$, 则 EF 的长是 (D)

A. 1
B. 2
C. 3
D. 4

答案： D

5. 如图, 六边形 ABCDEF 和六边形 GHIJKL 相似, 相似比为 2, 则下列结论正确的是 (C)
A. $∠E = 2∠K$
B. $2∠A = ∠G$
C. $AB = 2GH$
D. $2BC = HI$

答案： C

6. 如果四边形 ABCD 与四边形 $A'B'C'D'$ 相似, 且 $CD⊥BC,C'D'⊥B'C',∠B = 65^{\circ},∠A' = 135^{\circ}$, 根据图中的条件, 求出未知的 $x,y$ 及 $∠α$.

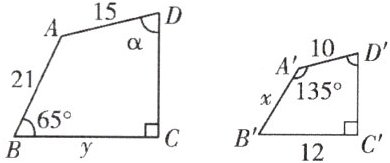
答案： 解: 依题意得, 四边形 $ABCD$ 与四边形 $A'B'C'D'$ 相似, 且 $CD \perp BC$, $C'D' \perp B'C'$,
$\therefore \angle \alpha = \angle D' = \angle D$, $\angle B = \angle B' = 65^\circ$, $\angle A = \angle A' = 135^\circ$, $\angle C = \angle C' = 90^\circ$, $\frac{AB}{A'B'} = \frac{BC}{B'C'} = \frac{AD}{A'D'}$,
$\therefore \angle \alpha = 360^\circ - \angle A - \angle B - \angle C = 70^\circ$,
又 $\because AB = 21$, $BC = y$, $AD = 15$, $A'B' = x$, $B'C' = 12$, $A'D' = 10$,
$\therefore \frac{21}{x} = \frac{y}{12} = \frac{15}{10}$, 解得 $x = 14$, $y = 18$.

7. 如图, 在长为 8 cm, 宽为 4 cm 的矩形中, 截去一个矩形, 使得留下的矩形 ABCD 与原矩形相似, 则留下的矩形 ABCD 的面积是 (C)
A. $2cm^{2}$
B. $4cm^{2}$
C. $8cm^{2}$
D. $16cm^{2}$

答案： C 解析: 依题意得, 矩形 $ABCD$ 与原矩形相似, $\therefore \frac{AD}{4} = \frac{4}{8}$, 解得 $AD = 2$, 则矩形 $ABCD$ 的面积为 $2 × 4 = 8 \, \text{cm}^2$. 故选 C.

8. 如图, 已知 $\triangle ADE \backsim \triangle ABC,AD = 2,BD = 3$. $\triangle ADE$ 与 $\triangle ABC$ 的相似比为$2:5$.

答案： $2:5$

9. 手工制作课上, 小红利用一些花布的边角料, 剪裁后装饰手工画, 下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边, 其中, 每个图案花边的宽度都相等, 那么, 每个图案中花边的内外边缘所围成的几何图形不一定相似的是 (D)

答案： D