《2025年正大图书练测考八年级数学下册鲁教版》

1. 下列图形，不是相似图形的一组是 （ ）

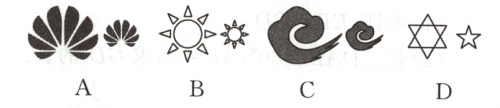
答案： D

2. 若$5x - 6y = 0$，且$xy\neq0$，则$\frac{5x + 6y}{10x - 4y}$的值等于 （ ）
A. $\frac{3}{2}$
B. 1
C. $\frac{2}{3}$
D. -1

答案： A

3. 如图，矩形$OABC\backsim$矩形$OA'B'C'$，$B'(10,5)$，$AA' = 1$，则$CC'$的长是 （ ）

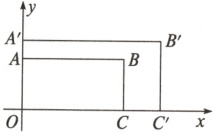
A. 1
B. 2
C. 3
D. 4

答案： B

4. 已知$x:4 = y:5 = z:6$，则$(x + y):(y + z)=$ （ ）
A. $2:3$
B. $4:5$
C. $9:11$
D. $5:11$

答案： C

5. 若一个矩形剪掉一个面积最大的正方形，剩下的小矩形与原来的矩形相似，且原矩形的较长边长为8 cm，则剩下的小矩形的较短边长为 ________cm. （ ）
A. $2\sqrt{5}$
B. $5\sqrt{5}-8$
C. $4\sqrt{5}-4$
D. $12 - 4\sqrt{5}$

答案： D

6. 如图，在$\triangle ABC$中，$\angle A = 90^{\circ}$，$AB = 6$，$BC = 10$，$\angle ABC$的平分线交$AC$于点$D$，与$BC$的垂线$CE$相交于点$E$，则$BD:DE$为 （ ）

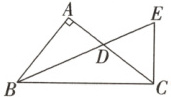
A. $3:2$
B. $5:3$
C. $4:3$
D. $2:1$

答案：
解析：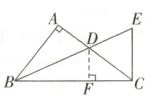
如图，过点D作DF⊥BC于点F.
∵∠A = 90°，AB = 6，BC = 10，
∴DA⊥BA，AC = $\sqrt{BC^{2}-AB^{2}}=\sqrt{10^{2}-6^{2}} = 8$.
∵BD平分∠ABC，DF⊥BC，
∴DA = DF.
∵$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle BCD}$，
∴$\frac{1}{2}AB\cdot AC=\frac{1}{2}AB\cdot DA+\frac{1}{2}BC\cdot DF$，
∴6×8 = 6DF + 10DF，解得DF = 3，
∴DA = 3，
∴CD = AC - DA = 8 - 3 = 5，
∴CF = $\sqrt{CD^{2}-DF^{2}}=\sqrt{5^{2}-3^{2}} = 4$，
∴BF = BC - CF = 10 - 4 = 6.
∵DF⊥BC，CE⊥BC，
∴DF//CE，
∴$\frac{BD}{DE}=\frac{BF}{CF}=\frac{6}{4}=\frac{3}{2}$，
即BD：DE = 3：2. 故选A.

7. 若$2x = y$，则$\frac{2x + y}{x - 3y}$的值是________.

答案： $-\frac{4}{5}$

8. [数学文化]《九章算术》之“粟米篇”中记载了我国古代的“粟米之法”：“粟率五十，粝米三十……”（粟指带壳的谷子，粝米指糙米），其意为：“50单位的粟，可换得30单位的粝米……”. 问题：有3斗的粟(1斗 = 10升)，若按照此“粟米之法”，则可以换得的粝米为 ________升.

答案： 18

9. 已知$\frac{a}{b}=\frac{3}{5}$，则$\frac{b + a}{b - a}=$________.

答案： 4

10. 已知$\frac{2x + y}{3}=\frac{x + 3y}{5}$，求$\frac{x + 2y}{2x - 3y}$的值.

答案： 解：
∵$\frac{2x + y}{3}=\frac{x + 3y}{5}$，
∴5(2x + y)=3(x + 3y)，
整理，得$x=\frac{4}{7}y$，
∴$\frac{x + 2y}{2x - 3y}=\frac{\frac{4}{7}y+2y}{2\times\frac{4}{7}y - 3y}=-\frac{18}{13}$.

11. 若$\frac{2}{x}=\frac{3}{y}=\frac{5}{z}$，且$3x + 2y - z = 14$，求$x$的值.

答案： 解：由$\frac{2}{x}=\frac{3}{y}=\frac{5}{z}$，得$y=\frac{3}{2}x$，$z=\frac{5}{2}x$.
把$y=\frac{3}{2}x$，$z=\frac{5}{2}x$代入3x + 2y - z = 14，
得$3x + 3x-\frac{5}{2}x = 14$，解得x = 4.