《2025年正大图书练测考八年级数学下册鲁教版》

1. (2024·东营东营区月考)下列方程中，关于x的一元二次方程是 （ ）
A. $\sqrt{5}x^{2}-\sqrt{2}xy - 7 = 0$
B. $-x^{2}+5x - 7 = 0$
C. $ax^{2}+bx + c = 0$
D. $x(x - 3)=2 + x^{2}$

答案： B 解析：A. 含有两个未知数，不是关于x的一元二次方程，不符合题意；
B. 是关于x的一元二次方程，符合题意；
C. 当a = 0时，不是关于x的一元二次方程，不符合题意；
D. 化简后未知数最高次数是1，不是关于x的一元二次方程，不符合题意. 故选B.

2. 关于x的方程$(m + 1)x^{2}+2mx - 3 = 0$是一元二次方程，则m的取值是 （ ）
A. 任意实数
B. $m\neq1$
C. $m\neq - 1$
D. $m＞1$

答案： C

3. (2023·济南商河县期末)将一元二次方程$(x + a)^{2}=b$，化成$x^{2}-8x - 5 = 0$的形式，则a，b的值分别是 （ ）
A. $-4,21$
B. $-4,11$
C. $4,21$
D. $-8,69$

答案： A 解析：
∵(x + a)² = b，
∴x² + 2ax + a² = b，
∴x² + 2ax + a² - b = 0.
由题意，得2a = - 8，a² - b = - 5，
解得a = - 4，b = 21. 故选A.

4. 一元二次方程$x^{2}+4x = 3$的一次项系数、二次项系数、常数项的和是 （ ）
A. 1
B. 8
C. 7
D. 2

答案： D

5. 一个关于x的一元二次方程，它的二次项系数为2，一次项系数为3，常数项为 - 5，则这个一元二次方程是______________.

答案： 2x² + 3x - 5 = 0

6.《九章算术》中记载一个数学问题，其大意为：有一个长方形的门框，它的高比宽多6.8尺，对角线长10尺，问它的高与宽各是多少？设门框高为x尺，依题意列方程为 （ ）
A. $x^{2}+(x + 6.8)^{2}=10^{2}$
B. $x^{2}+(x - 6.8)^{2}=10^{2}$
C. $x(x + 6.8)=10^{2}$
D. $x(x - 6.8)=10^{2}$

答案： B

7. (2024·眉山)眉山市东坡区永丰村是“天府粮仓”示范区，该村的“智慧春耕”让生产更高效，提升了水稻亩产量，水稻亩产量从2021年的670千克增长到了2023年的780千克，该村水稻亩产量年平均增长率为x，则可列方程为 （ ）
A. $670\times(1 + 2x)=780$
B. $670\times(1 + x)^{2}=780$
C. $670\times(1 + x^{2})=780$
D. $670\times(1 + x)=780$

答案： B

8. 小张的书法作品荣获学校书法比赛一等奖. 作品尺寸如图所示：书法作品长5尺，宽3尺；将书法作品贴在一张矩形装裱纸的正中央，书法作品四周外露装裱纸的宽度均相同；矩形装裱纸的面积为书法作品面积的2倍. 设书法作品四周外露装裱纸的宽度为x尺，下面所列方程正确的是 （ ）

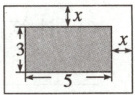
A. $(5 + 2x)(3 + 2x)=2\times5\times3$
B. $(5 + x)(3 + x)=2\times5\times3$
C. $2(5 + 2x)(3 + 2x)=5\times3$
D. $(5 + 2x)(3 + 2x)=5\times3$

答案： A

9. 若一元二次方程$2x^{2}-(m + 1)x + 1 = x$的一次项系数为 - 3，则m的值为________.

答案： 1

10. 方程$(m + 2)x^{|m|}+3mx + 1 = 0$是关于x的一元二次方程，则 （ ）
A. $m=\pm2$
B. $m = 2$
C. $m = - 2$
D. $m\neq\pm2$

答案： B