第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1.(2024·威海荣成市期中)如图,Rt△ACB中,∠C = 90°,AC = 7,BC = 5,点P从点B出发向终点C以1个单位长度/s移动,点Q从点C出发向终点A以2个单位长度/s移动,P,Q两点同时出发,一点先到达终点时P,Q两点同时停止,则______秒后,△PCQ的面积等于4.

A. 1
B. 2
C. 4
D. 1或4

A. 1
B. 2
C. 4
D. 1或4
答案:
1.A 解析:设t秒后,△PCQ的面积等于4.
由题意,得BP=t,CQ=2t,则CP=5−t.
∵SPCQ=$\frac{1}{2}$CQ.CP,
∴4=$\frac{1}{2}$×2t.(5−t),整理,得t²−5t+4=0,
解得t1=1,t2=4(不合题意,舍去),
即1秒后,△PCQ的面积等于4.故选A.
由题意,得BP=t,CQ=2t,则CP=5−t.
∵SPCQ=$\frac{1}{2}$CQ.CP,
∴4=$\frac{1}{2}$×2t.(5−t),整理,得t²−5t+4=0,
解得t1=1,t2=4(不合题意,舍去),
即1秒后,△PCQ的面积等于4.故选A.
2. 如图,将边长为12 cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A'B'C',若两个三角形重叠部分的面积为32 cm²,则它移动的距离AA'等于
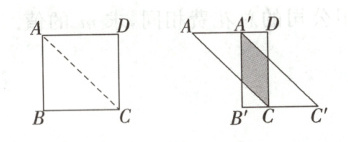
A. 4 cm
B. 8 cm
C. 6 cm
D. 4 cm或8 cm

A. 4 cm
B. 8 cm
C. 6 cm
D. 4 cm或8 cm
答案:
2.D 解析:设AA'=xcm,则A'D=(12−
x)cm.
∵题图中四边形ABCD是正方形,
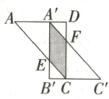
∴∠D=∠DAB=90°,∠DAC=∠BAC=
45°.
∵如图,△A'B'C'由△ABC沿着AD
方向平移得到,
∴∠B'A'Cy=45°,A'B'⊥AD,
∴A'E//CF,∠A'EA=45°,
∴AA'=A'E=xcm,∠B'A'C'=∠A'EA,
∴A'F//EC,
∴四边形A'ECF为平行四边形,所以SA、ECF=AE×A'D=x(12−x)=32,解得x=4或8.
故选D.
2.D 解析:设AA'=xcm,则A'D=(12−
x)cm.
∵题图中四边形ABCD是正方形,

∴∠D=∠DAB=90°,∠DAC=∠BAC=
45°.
∵如图,△A'B'C'由△ABC沿着AD
方向平移得到,
∴∠B'A'Cy=45°,A'B'⊥AD,
∴A'E//CF,∠A'EA=45°,
∴AA'=A'E=xcm,∠B'A'C'=∠A'EA,
∴A'F//EC,
∴四边形A'ECF为平行四边形,所以SA、ECF=AE×A'D=x(12−x)=32,解得x=4或8.
故选D.
3. 如图,在矩形ABCD中,AB = 16 cm,BC = 6 cm,点P从点A出发沿AB以3 cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2 cm/s的速度向点D移动. 设运动时间为t s,当PQ = 10 cm时,t =

A. $\frac{8}{3}$
B. $\frac{8}{5}$或4
C. $\frac{8}{5}$或$\frac{24}{5}$
D. 4

A. $\frac{8}{3}$
B. $\frac{8}{5}$或4
C. $\frac{8}{5}$或$\frac{24}{5}$
D. 4
答案:
3.C 解析:设P,Q两点从出发经过ts时,点P,
Q间的距离是10cm.如图,作PH⊥CD,垂足
为H,
 则易得PH=BC=6,PQ=10,HQ=|16−5t|.
则易得PH=BC=6,PQ=10,HQ=|16−5t|.
∵PH²+HQ²=PQ²,
∴6²+(16−5t)²=10²,解得t1=$\frac{8}{5}$,t2=$\frac{24}{5}$.
∴P,Q两点从出发经过$\frac{8}{5}$s或$\frac{24}{5}$s时,点P,Q间的距离是10cm.故选C.
3.C 解析:设P,Q两点从出发经过ts时,点P,
Q间的距离是10cm.如图,作PH⊥CD,垂足
为H,
 则易得PH=BC=6,PQ=10,HQ=|16−5t|.
则易得PH=BC=6,PQ=10,HQ=|16−5t|.∵PH²+HQ²=PQ²,
∴6²+(16−5t)²=10²,解得t1=$\frac{8}{5}$,t2=$\frac{24}{5}$.
∴P,Q两点从出发经过$\frac{8}{5}$s或$\frac{24}{5}$s时,点P,Q间的距离是10cm.故选C.
4. 如图,∠AOB = 90°,OA = 36 cm,OB = 12 cm,一个小球从点A出发沿着AO方向滚向点O,另一小球立即从点B出发,沿BC匀速前进拦截小球,恰好在点C处截住了小球. 若两个小球滚动的速度相等,则另一个小球滚动的路程BC是______cm.


答案:
4.20 解析:由题意,知∠AOB=90°,OA=36cm,OB=
12cm.设AC=xcm,则OC=(36−x)cm,
在Rt△BOC中,BC= $\sqrt{OC²+OB²}$=√(36−x)²+12².
∵两个小球滚动的速度相等,设速度为,根据题意,一个小球从点A出发,另一小球立即从点B出发,恰好在点C 处截住,可知两小球运动时间相等,
∴BC=AUC,
∴BC=AC,
∴ $\sqrt{(36−x)²+12²}$=x,解得x=20,
∴BC=20cm.
12cm.设AC=xcm,则OC=(36−x)cm,
在Rt△BOC中,BC= $\sqrt{OC²+OB²}$=√(36−x)²+12².
∵两个小球滚动的速度相等,设速度为,根据题意,一个小球从点A出发,另一小球立即从点B出发,恰好在点C 处截住,可知两小球运动时间相等,
∴BC=AUC,
∴BC=AC,
∴ $\sqrt{(36−x)²+12²}$=x,解得x=20,
∴BC=20cm.
5. 如图所示,甲、乙两点分别从直径的两端点A,B同时出发,并分别以顺时针的方向沿圆周运动. 甲运动的路程s(cm)与时间t(s)满足s = $\frac{1}{2}t^{2}+\frac{3}{2}t$(t≥0),乙以4 cm/s的速度匀速运动,半圆的长度为21 cm.
(1)甲运动6 s后的路程是______;
(2)甲从运动开始到第一次追上乙时,它们运动了多长时间?
(3)甲从运动开始到第二次追上乙时,它们运动了多长时间?
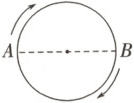
(1)甲运动6 s后的路程是______;
(2)甲从运动开始到第一次追上乙时,它们运动了多长时间?
(3)甲从运动开始到第二次追上乙时,它们运动了多长时间?

答案:
5.解:
(1)27cm
(2)由题,可知甲从运动开始到第一次追上乙时,甲走过的路程比乙走过的路程多21cm,甲走过的路程为($\frac{1}{2}$t²+$\frac{3}{2}$t)cm,乙走过的路程为4tcm,
∴$\frac{1}{2}$t²+$\frac{3}{2}$t−4t=21,
解得t1=$\frac{5+\sqrt{193}}{2}$,t2=$\frac{5−\sqrt{193}}{2}$(舍去).
∴甲从运动开始到第一次追上乙时,它们运动了$\frac{5+\sqrt{193}}{2}$S.
(3)由题,可知甲从运动开始到第二次追上乙时,甲走过的路比乙走过的路程多21×3=63(cm),甲走过的路程为($\frac{1}{2}$t²+$\frac{3}{2}$t)cm,乙走过的路程为4tcm,
∴$\frac{1}{2}$t²+$\frac{3}{2}$t−4t=63,解得t1=14,t2=−9(舍去),
∴甲从运动开始到第二次追上乙时,它们运动了14s.
(1)27cm
(2)由题,可知甲从运动开始到第一次追上乙时,甲走过的路程比乙走过的路程多21cm,甲走过的路程为($\frac{1}{2}$t²+$\frac{3}{2}$t)cm,乙走过的路程为4tcm,
∴$\frac{1}{2}$t²+$\frac{3}{2}$t−4t=21,
解得t1=$\frac{5+\sqrt{193}}{2}$,t2=$\frac{5−\sqrt{193}}{2}$(舍去).
∴甲从运动开始到第一次追上乙时,它们运动了$\frac{5+\sqrt{193}}{2}$S.
(3)由题,可知甲从运动开始到第二次追上乙时,甲走过的路比乙走过的路程多21×3=63(cm),甲走过的路程为($\frac{1}{2}$t²+$\frac{3}{2}$t)cm,乙走过的路程为4tcm,
∴$\frac{1}{2}$t²+$\frac{3}{2}$t−4t=63,解得t1=14,t2=−9(舍去),
∴甲从运动开始到第二次追上乙时,它们运动了14s.
查看更多完整答案,请扫码查看


