《2025年正大图书练测考八年级数学下册鲁教版》

1. 四边形ABCD的对角线AC，BD互相平分，要使它成为矩形，可添加条件 （ ）
A. AB = CD
B. AC = BD
C. AB//CD
D. AC⊥BD

答案： B 解析：由四边形ABCD的对角线AC，BD互相平分，可知四边形ABCD为平行四边形. 添加条件AC = BD，可证明四边形ABCD是矩形，故B符合题意. A，C，D选项均无法证明四边形ABCD是矩形. 故选B.

2. 如图，为了检查平行四边形书架ABCD的侧边是否与上、下边都垂直，工人师傅用一根绳子比较了其对角线AC，BD的长度，若二者长度相等，则该书架的侧边与上、下边都垂直，请你说出其中的数学原理____________________.

答案： 对角线相等的平行四边形是矩形，矩形的四个角都是直角

3. 如图，平行四边形ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，DF⊥AC于点F，且AE = DF. 求证：四边形ABCD是矩形.

答案： 证明：
∵AE⊥BD，DF⊥AC，
∴∠AEO = ∠DFO = 90°.
又
∵AE = DF，∠AOE = ∠DOF，
∴△AEO≌△DFO(AAS)，
∴AO = DO.
∵四边形ABCD是平行四边形，
∴AO = CO = DO = BO，
∴AC = BD，
∴四边形ABCD是矩形.

4. 在数学活动课上，老师让同学们判断一个四边形门框是否为矩形，下面是一个学习小组拟定的方案，其中正确的方案是 （ ）
A. 测量其中三个角是否为直角
B. 测量两组对边是否相等
C. 测量对角线是否相互平分
D. 测量对角线是否相等

答案： A

5. [教材P15做一做变式]
如图，一个平行四边形的活动框架，对角线是两根橡皮筋. 若改变框架的形状，则∠α也随之变化，两条对角线长度也在发生改变. 当∠α为________时，两条对角线长度相等.

答案： 90 解析：根据题意，得∠α = 90°时，四边形为矩形，故两条对角线相等.

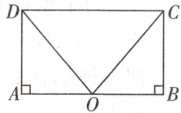
6.（2024·长春）如图，在四边形ABCD中，∠A = ∠B = 90°，O是边AB的中点，∠AOD = ∠BOC. 求证：四边形ABCD是矩形.

答案： 解：
∵O是边AB的中点，
∴OA = OB.
在△AOD和△BOC中，$\begin{cases}∠AOD = ∠BOC，\\OA = OB，\\∠A = ∠B.\end{cases}$
∴△AOD≌△BOC(ASA)，
∴DA = CB.
∵∠A = ∠B = 90°，
∴DA//CB，
∴四边形ABCD是平行四边形.
又
∵∠A = 90°，
∴四边形ABCD是矩形.

7. 在一组对边平行的四边形中，下列条件中，可判定这个四边形是矩形的是 （ ）
A. 另一组对边相等，对角线相等
B. 另一组对边相等，对角线互相垂直
C. 另一组对边平行，对角线相等
D. 另一组对边平行，对角线互相垂直

答案： C 解析：此题因对矩形的判定方法理解错误而出错. 在一组对边平行的前提下，再找该组对边相等或另一组对边平行即可判定这个四边形为平行四边形，再结合对角线相等即可判定这个四边形是矩形. 故选C.

8. 如图，直角三角形ABC的面积为4，点D是斜边AB的中点，过点D作DE⊥AC于点E，DF⊥BC于点F，则四边形DECF的面积为 （ ）

A. 1
B. 2
C. 2.5
D. 3

答案： B

9. 四边形的两条对角线________时，连接四条边的中点，得到的新四边形是矩形. （ ）
A. 垂直
B. 相等
C. 垂直平分
D. 相等平分

答案： A