《2025年正大图书练测考八年级数学下册鲁教版》

1. 将一个三角形的各边都缩小到原来的$\frac{1}{2}$后，得到三角形与原三角形（ ）
A. 一定不相似
B. 不一定相似
C. 无法判定是否相似
D. 一定相似

答案： D

2. 已知$\triangle ABC$的三边长分别为$1$，$\sqrt{2}$，$\sqrt{5}$，$\triangle DEF$的三边长分别$\sqrt{3}$，$\sqrt{6}$，$\sqrt{15}$，则$\triangle ABC$与$\triangle DEF$（ ）
A. 一定相似
B. 一定不相似
C. 不一定相似
D. 无法判定是否相似

答案： A

3.（2024·滨州邹平市期末）如图所示，网格中相似的两个三角形是（ ）

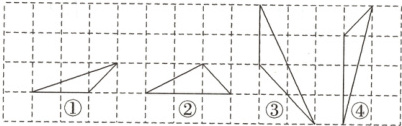
A. ①与③
B. ②与③
C. ①与④
D. ③与④

答案： A 解析：图①的三边为$2,\sqrt{10},\sqrt{2}$；
图②的三边为$3,\sqrt{5},\sqrt{2}$；
图③的三边为$2,2\sqrt{2},2\sqrt{5}$；
图④的三边为$3,\sqrt{17},\sqrt{2}$。
$\because\frac{2}{2\sqrt{2}}=\frac{\sqrt{2}}{2}=\frac{\sqrt{10}}{2\sqrt{5}}=\frac{\sqrt{2}}{2}$，
$\therefore$①与③相似. 故选A.

4. 如图，在正方形网格中有三个三角形，分别是$\triangle EBC$，$\triangle CDB$，$\triangle DEB$，其中与$\triangle ABC$相似的是______.

答案： $\triangle DEB$

5. 如图，在$\triangle ABC$中，$D$，$E$，$F$分别是$CA$，$AB$，$BC$的中点，则$\triangle ABC$与$\triangle FDE$相似吗？为什么？

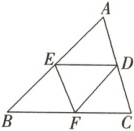
答案： 解：相似. $\because D,E,F$分别是$CA,AB,BC$的中点，
$\therefore DE,DF,EF$是$\triangle ABC$的中位线，
$\therefore\frac{DE}{BC}=\frac{DF}{AB}=\frac{EF}{AC}=\frac{1}{2}$，
$\therefore\triangle ABC\sim\triangle FDE$.

6. 如图，点$O$是$\triangle ABC$外的一点，分别在射线$OA$，$OB$，$OC$上取一点$A'$，$B'$，$C'$，使得$\frac{OA'}{OA}=\frac{OB'}{OB}=\frac{OC'}{OC}=3$，连接$A'B'$，$B'C'$，$C'A'$，所得$\triangle A'B'C'$与$\triangle ABC$是否相似？证明你的结论.

答案： 解：$\triangle A'B'C'\sim\triangle ABC$.
证明：$\because\frac{OA'}{OA}=\frac{OC'}{OC}=3,\angle A'OC'=\angle AOC$，
$\therefore\triangle A'OC'\sim\triangle AOC$，
$\therefore\frac{A'C'}{AC}=\frac{OA'}{OA}=3$，
同理$\frac{B'C'}{BC}=3,\frac{A'B'}{AB}=3$，
$\therefore\frac{A'C'}{AC}=\frac{B'C'}{BC}=\frac{A'B'}{AB},\therefore\triangle A'B'C'\sim\triangle ABC$.

7.（大庆中考）已知两个直角三角形的三边长分别为$3$，$4$，$m$和$6$，$8$，$n$，且这两个直角三角形不相似，则$m + n$的值为（ ）
A. $10+\sqrt{7}$或$5 + 2\sqrt{7}$
B. $15$
C. $10+\sqrt{7}$
D. $15 + 3\sqrt{7}$

答案： A 解析：在第一个直角三角形中，若$m$是直角边，则$m = \sqrt{4^{2}-3^{2}}=\sqrt{7}$；
若$m$是斜边，则$m = \sqrt{4^{2}+3^{2}}=5$.
在第二个直角三角形中，若$n$是直角边，则$n = \sqrt{8^{2}-6^{2}}=\sqrt{28}=2\sqrt{7}$；
若$n$是斜边，则$n = \sqrt{8^{2}+6^{2}}=10$.
又因为两个直角三角形不相似，故$m = 5$和$n = 10,m=\sqrt{7}$和$n = 2\sqrt{7}$不能同时取，
$\therefore$当$m = 5,n = 2\sqrt{7}$时，$m + n = 5+2\sqrt{7}$；
当$m=\sqrt{7},n = 10$时，$m + n = 10+\sqrt{7}$.
故选A.

8. 在如图所示的象棋盘（各个小正方形的边长均相等）中，根据“马走日”的规则，“马”落在下列哪个位置，能使“马”“車”“炮”所在位置的格点构成的三角形与“帥”“相”“兵”所在位置的格点构成的三角形相似？（ ）

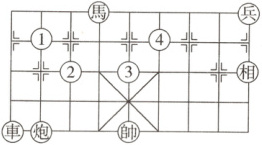
A. ①
B. ②
C. ③
D. ④

答案： B

9. 如图，在正方形网格中有$5$个格点三角形，分别是：①$\triangle ABC$，②$\triangle ACD$，③$\triangle ADE$，④$\triangle AEF$，⑤$\triangle AGH$，其中与⑤相似的三角形是（ ）

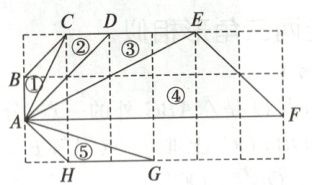
A. ①③
B. ①④
C. ②④
D. ①③④

答案： A