《2025年正大图书练测考八年级数学下册鲁教版》

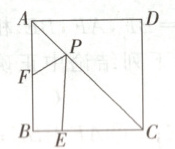
10. 如图，正方形ABCD的边长为4，E为BC上的一点，BE = 1，F为AB上的一点，AF = 2，P为AC上的一个动点，则PF + PE的最小值为______.

答案：
$\sqrt{17}$　解析:如图，在AD上取一点M，
　使得AM=2,易知点F,M关于直线
AC对称.连接MP，则FP=MP.连接
EM,交AC于点P',连接P'F,易得
　ME=P'F+P'E,即当P运动至P'处
时，PF+PE有最小值,EM的长为PF十PE的最小值.过点M作MN⊥BC于点N,由题意易知EN=BN一
BE=AM−BE=2−1=1,MN=4,所以EM=
　　$\sqrt{EN²+MN²}$=　$\sqrt{1²+4²}$=　$\sqrt{17}$

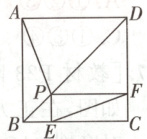
11. 如图，P为正方形ABCD的对角线BD上的任一点，过点P作PE⊥BC于点E，作PF⊥CD于点F，连接EF，给出以下4个结论：①△FDP是等腰直角三角形，②AP = EF，③∠PFE = ∠BAP，④AD = PD. 其中正确的有 （ ）

A. 1个
B. 2个
C. 3个
D. 4个

答案： C

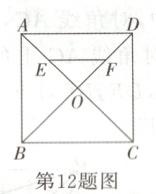
12.（2024·吉林）如图，正方形ABCD的对角线AC，BD相交于点O，点E是OA的中点，点F是OD上一点. 连接EF. 若∠FEO = 45°，则$\frac{EF}{BC}$的值为______.

答案： $\frac{1}{2}$

13.（2024·济南莱芜区期中）如图，直线l经过正方形ABCD的顶点C，点B，D到直线l的距离分别是2，1，则正方形的边长为______.

答案： $\sqrt{5}$　解析:在正方形ABCD中,CD=CB=AB,∠DCB=
　∠ABC=90°.
　
∵DF⊥CF,BE⊥CE,
　
∴∠CFD=∠CEB=90°,∠CDF+∠DCF=90°.
　
∵∠DCF+∠BCE=90°,
∴∠CDF=∠BCE.
　在△CFD和△BEC中，
　∠CFD=∠BEC,∠CDF=∠BCE,CD=BC,
　
∴△CFD≌△BEC(AAS),
　
∴DF=CE=1,CF=BE=2.
　在Rt△BEC中，由勾股定理，得BC²²=CE²+BE²,即
BC²=1²+2²,则BC=　　$\sqrt{5}$二
　故正方形的边长是　　$\sqrt{5}$

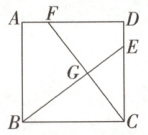
14.（2024·威海荣成市期中）如图，正方形ABCD中，点E，F分别在边CD，AD上，BE与CF交于点G. 若BC = 8，DE = AF = 2，则GF的长为______.

答案： $\frac{26}{5}$　解析:在正方形ABCD中,BC=8,
　
∴BC=CD=AD=8,∠BCE=∠CDF=90°.
　
∵DE=AF=2,
∴DF=CE=6,
　
∴BE=CF=　$\sqrt{6²+82}$=10.
BC=CD,
　在△BCE和△CDF中，{∠BCE=∠CDF,
　　　　　　　　　　　　E=DF,
　
∴△BCE≌△CDF(SAS),
∴∠CBE=∠DCF,
　
∴∠CBE+∠CEB=∠ECG+∠CEB=90°,
　
∴∠CGE=90°.
　
∵S△BCE=$\frac{1}{2}$BC.CE=$\frac{1}{2}$BE.CG,
　
∴CG=$\frac{BC.CE}{BE}$=$\frac{8×6}{10}$=$\frac{24}{5}$,
　
∴GF=CF−CG=10−$\frac{24}{5}$=$\frac{26}{5}$

15. 如图，正方形ABCD的对角线AC，BD相交于点O，E，G分别是OB，OC上的点，CE与DG的延长线相交于点F. 若DF⊥CE. 求证：OG = OE.

答案： 证明:
∵四边形ABCD是正方形，
　
∴OC=OD,AC⊥BD,
∴∠COE=∠DOG=90°,
　
∴∠CEO+∠ECO=90°.
　
∵DF⊥CE,
∴∠CEO+∠EDF=90°,
　
∴∠ECO=∠EDF.
　　　　　　　　　　　　∠COE=∠DOG,
　　在△CEO与△DGO中，{OC=OD,
　　　　　　　　　　　　∠ECO=∠GDO,
　
∴△CEO△DGO(ASA),
∴OG=OE.

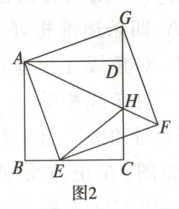
16. 如图1，四边形ABCD是正方形，点E是BC上一点，连接AE，以AE为一边作正方形AEFG，连接DG.
(1)求证：DG = BE.
(2)如图2，连接AF交CD于点H，连接EH，请探究EH，BE，DH三条线段之间的数量关系，并说明理由.

答案：
(1)证明:
∵四边形ABCD是正方形，
　
∴∠DAB=∠B=∠ADC=90°,AB=AD,
　
∴∠BAE+∠EAD=90°.
　
∵四边形AEFG是正方形，
　
∴∠EAD+∠DAG=∠EAG=90°,AE=AG,
　
∴∠BAE+∠EAD=∠EAD+∠DAG,
　
∴∠BAE=∠DAG.
AE=AG,
　　在△BAE和△DAG中，{∠BAE=∠DAG,
AB=AD,
　
∴△BAE≌△DAG(SAS),
∴DG=BE.
(2)解:BE+DH=EH.
理由:
∵△BAE≌△DAG,
∴∠ADG=∠B=90°,BE=DG.
∴∠ADG+∠ADH=180°,
∴点H,D,G共线
∵四边形AEFG是正方形，
∴∠EAH=∠GAH=45°.
AE=AG,
在△EAH和△GAH中，{∠EAH=∠GAH,
AH=AH,
∴△EAH≌△GAH(SAS),
∴EH=GH.
∵DG+DH=GH,
∴BE+DH=EH.