第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
7. 用配方法解下列方程,配方错误的是 ( )
A. $x^{2}+2x - 99 = 0$化为$(x + 1)^{2}=100$
B. $2x^{2}-7x - 4 = 0$化为$(x-\frac{7}{4})^{2}=\frac{81}{16}$
C. $x^{2}+8x + 9 = 0$化为$(x + 4)^{2}=25$
D. $3x^{2}-4x - 2 = 0$化为$(x-\frac{2}{3})^{2}=\frac{10}{9}$
A. $x^{2}+2x - 99 = 0$化为$(x + 1)^{2}=100$
B. $2x^{2}-7x - 4 = 0$化为$(x-\frac{7}{4})^{2}=\frac{81}{16}$
C. $x^{2}+8x + 9 = 0$化为$(x + 4)^{2}=25$
D. $3x^{2}-4x - 2 = 0$化为$(x-\frac{2}{3})^{2}=\frac{10}{9}$
答案:
C
8. 当$x =$________时,代数式$3x^{2}-2x + 1$有________(填“最大值”或“最小值”),这个值是________.
答案:
$\frac{1}{3}$ 最小值 $\frac{2}{3}$
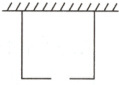
9. 学校计划利用一块空地修建一个学生自行车棚,其中一面靠墙,这堵墙的长度为12米,建造车棚的面积为80平方米,已知新建板墙的木板材料的总长为26米,为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门(如图),那么车棚的长与宽分别为多少米?

答案:
解:设垂直于墙的一边长为$x$米. 根据题意,得$x(26 - 2x + 2)=80$,解得$x_{1}=10,x_{2}=4$(不合题意,舍去).
$\therefore 26 - 2\times10 + 2 = 8$(米).
故车棚的长为10米,宽为8米.
$\therefore 26 - 2\times10 + 2 = 8$(米).
故车棚的长为10米,宽为8米.
10. [应用意识]【阅读材料】我们都知道$a^{2}+2ab + b^{2}=(a + b)^{2},a^{2}-2ab + b^{2}=(a - b)^{2}$,
于是:$-2x^{2}+40x + 5$
$=-2(x^{2}-20x)+5$
$=-2(x^{2}-2\cdot x\cdot10 + 10^{2}-10^{2})+5$
$=-2[(x - 10)^{2}-100]+5$
$=-2(x - 10)^{2}+205$.
又$\because(x - 10)^{2}\geq0$,
$\therefore-2(x - 10)^{2}\leq0$,
$\therefore-2(x - 10)^{2}+205\leq205$,
$\therefore-2x^{2}+40x + 5$有最大值205.
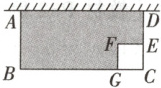
【解决问题】如图,某农户准备用长34米的铁栅栏围成一边靠墙(墙足够长)的矩形羊圈$ABCD$和一个边长为1米的正方形狗屋$CEFG$.设$AB = x$米.
(1)请用含$x$的代数式表示$BC$的长;(写出具体解题过程)
(2)设山羊活动范围即图中阴影部分的面积为$S$,试用含$x$的代数式表示$S$,并计算当$x = 5$时$S$的值;
(3)试求出山羊活动范围的面积$S$的最大值.
于是:$-2x^{2}+40x + 5$
$=-2(x^{2}-20x)+5$
$=-2(x^{2}-2\cdot x\cdot10 + 10^{2}-10^{2})+5$
$=-2[(x - 10)^{2}-100]+5$
$=-2(x - 10)^{2}+205$.
又$\because(x - 10)^{2}\geq0$,
$\therefore-2(x - 10)^{2}\leq0$,
$\therefore-2(x - 10)^{2}+205\leq205$,
$\therefore-2x^{2}+40x + 5$有最大值205.
【解决问题】如图,某农户准备用长34米的铁栅栏围成一边靠墙(墙足够长)的矩形羊圈$ABCD$和一个边长为1米的正方形狗屋$CEFG$.设$AB = x$米.
(1)请用含$x$的代数式表示$BC$的长;(写出具体解题过程)
(2)设山羊活动范围即图中阴影部分的面积为$S$,试用含$x$的代数式表示$S$,并计算当$x = 5$时$S$的值;
(3)试求出山羊活动范围的面积$S$的最大值.

答案:
解:
(1)依题意,得$AB = DC = x$米,$EF = FG = 1$米.
$AB + DC + BC + EF + FG = 34$米,
$\therefore 2x + BC + 2 = 34$,
$\therefore BC=(32 - 2x)$米.
(2)依题意,得$S = S_{矩形ABCD}-S_{正方形CEFG}=x(32 - 2x)-1=-2x^{2}+32x - 1$.
当$x = 5$时,$S=-2\times5^{2}+32\times5 - 1 = 109$(平方米).
(3)$S=-2x^{2}+32x - 1=-2(x^{2}-16x + 64)+127=-2(x - 8)^{2}+127$.
又$\because (x - 8)^{2}\geq0$,$\therefore - 2(x - 8)^{2}\leq0$,
$\therefore - 2(x - 8)^{2}+127\leq127$,
$\therefore$山羊活动范围的面积$S$的最大值是127平方米.
(1)依题意,得$AB = DC = x$米,$EF = FG = 1$米.
$AB + DC + BC + EF + FG = 34$米,
$\therefore 2x + BC + 2 = 34$,
$\therefore BC=(32 - 2x)$米.
(2)依题意,得$S = S_{矩形ABCD}-S_{正方形CEFG}=x(32 - 2x)-1=-2x^{2}+32x - 1$.
当$x = 5$时,$S=-2\times5^{2}+32\times5 - 1 = 109$(平方米).
(3)$S=-2x^{2}+32x - 1=-2(x^{2}-16x + 64)+127=-2(x - 8)^{2}+127$.
又$\because (x - 8)^{2}\geq0$,$\therefore - 2(x - 8)^{2}\leq0$,
$\therefore - 2(x - 8)^{2}+127\leq127$,
$\therefore$山羊活动范围的面积$S$的最大值是127平方米.
查看更多完整答案,请扫码查看


