第97页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1. 如图,四边形ABCD∽四边形EFGH,∠E = 85°,∠G = 90°,∠D = 120°,则∠B等于 ( )


A. 55°
B. 65°
C. 75°
D. 85°


A. 55°
B. 65°
C. 75°
D. 85°
答案:
B
2. 在比例尺为1 : 8000的某学校地图上,如果矩形运动场的图上尺寸是1 cm×2 cm,那么矩形运动场的实际尺寸应为 ( )
A. 80 m×160 m
B. 8 m×16 m
C. 800 m×160 m
D. 80 m×800 m
A. 80 m×160 m
B. 8 m×16 m
C. 800 m×160 m
D. 80 m×800 m
答案:
A
3. 如图,五边形ABCDE∽五边形A'B'C'D'E',则五边形ABCDE与五边形A'B'C'D'E'的相似比是________.


答案:
2:1
4.(2024·连云港)下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为 ( )

A. 甲和乙
B. 乙和丁
C. 甲和丙
D. 甲和丁

A. 甲和乙
B. 乙和丁
C. 甲和丙
D. 甲和丁
答案:
D
5. 下列说法正确的是 ( )
A. 所有的菱形都是相似形
B. 对应边成比例的两个多边形相似
C. 对应角相等的两个多边形相似
D. 所有的正方形都是相似形
A. 所有的菱形都是相似形
B. 对应边成比例的两个多边形相似
C. 对应角相等的两个多边形相似
D. 所有的正方形都是相似形
答案:
D解析:A.所有的菱形因为对应角不一定相等,所以不一定是相似形,故此选项错误;
B.对应边成比例的两个多边形因为对应角不一定相等,所以不一定相似,故此选项错误;
C.对应角相等的两个多边形因为对应边的比值不一定相等,所以不一定相似,故此选项错误;
D.所有的正方形对应边成比例且对应角相等,所以都是相似形,故此选项正确.故选D.
B.对应边成比例的两个多边形因为对应角不一定相等,所以不一定相似,故此选项错误;
C.对应角相等的两个多边形因为对应边的比值不一定相等,所以不一定相似,故此选项错误;
D.所有的正方形对应边成比例且对应角相等,所以都是相似形,故此选项正确.故选D.
6. [教材P96随堂练习T1变式]如图,有三个矩形,其中是相似图形的是 ( )
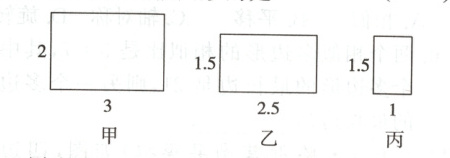
A. 甲和乙
B. 甲和丙
C. 乙和丙
D. 甲、乙和丙

A. 甲和乙
B. 甲和丙
C. 乙和丙
D. 甲、乙和丙
答案:
B
7. 如图,在四边形ABCD的边AB上任取一点O(不与点A,B重合),连接OC,OD,分别取OA,OB,OC,OD的中点A',B',C',D',连接A'D',D'C',C'B',四边形A'B'C'D'与四边形ABCD相似吗?为什么?


答案:
解:四边形A'B'C'D'与四边形ABCD相似,理由如下:
如图,
∵A',D'是OA,OD的中点,
∴A'D'/AD,A'D'=$\frac{1}{2}$AD,
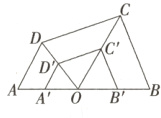
∴$\frac{A'D}{AD}$=$\frac{1}{2}$.
同理$\frac{C'D}{CD}$=$\frac{B'C}{BC}$=$\frac{A'B}{AB}$=$\frac{1}{2}$.
∵A'D'/AD,
∴∠OA'D'=∠OAD,∠OD'A'=∠ODA.
同理∠OD'C'=∠ODC,∠OC'D'=∠OCD,∠OC'B'=
∠OCB,∠OB'C'=∠OBC,
∴∠OA'D'=∠OAD,∠A'D'C'=∠ADC,∠D'C'B'=
∠DCB,∠OB'C'=∠OBC,
∴四边形A'B'C'D'与四边形ABCD相似.
解:四边形A'B'C'D'与四边形ABCD相似,理由如下:
如图,
∵A',D'是OA,OD的中点,
∴A'D'/AD,A'D'=$\frac{1}{2}$AD,

∴$\frac{A'D}{AD}$=$\frac{1}{2}$.
同理$\frac{C'D}{CD}$=$\frac{B'C}{BC}$=$\frac{A'B}{AB}$=$\frac{1}{2}$.
∵A'D'/AD,
∴∠OA'D'=∠OAD,∠OD'A'=∠ODA.
同理∠OD'C'=∠ODC,∠OC'D'=∠OCD,∠OC'B'=
∠OCB,∠OB'C'=∠OBC,
∴∠OA'D'=∠OAD,∠A'D'C'=∠ADC,∠D'C'B'=
∠DCB,∠OB'C'=∠OBC,
∴四边形A'B'C'D'与四边形ABCD相似.
8. 四边形ABCD与四边形A₁B₁C₁D₁相似,相似比为2 : 3,四边形A₁B₁C₁D₁与四边形A₂B₂C₂D₂相似,相似比为5 : 4,则四边形ABCD与四边形A₂B₂C₂D₂相似,且相似比为 ( )
A. 5 : 6
B. 6 : 5
C. 5 : 6或6 : 5
D. 8 : 15
A. 5 : 6
B. 6 : 5
C. 5 : 6或6 : 5
D. 8 : 15
答案:
A 解析:
∵四边形ABCD与四边形AlBlClD1的相似比为2:3=10:15,四边形A1B1C1D1与四边形A2B2C2D2 的相似比为5:4=15:12,,
∴四边形ABCD与四边形
A2B2C2D2的相似比为10:12=5:6.
∵四边形ABCD与四边形AlBlClD1的相似比为2:3=10:15,四边形A1B1C1D1与四边形A2B2C2D2 的相似比为5:4=15:12,,
∴四边形ABCD与四边形
A2B2C2D2的相似比为10:12=5:6.
查看更多完整答案,请扫码查看


