《2025年正大图书练测考八年级数学下册鲁教版》

11. [教材P87随堂练习T3变式]若a，b，b，c是成比例线段，其中a = 3，c = 12，则线段b的长为 （ ）
A. 2
B. 4
C. 6
D. 15

答案： C

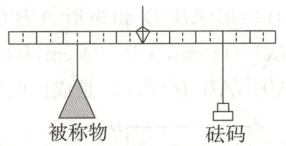
12. [跨学科]《九章算术》中记载，战国时期的铜衡杆，其形式既不同于天平衡杆，也异于秤杆. 衡杆正中有拱肩提纽和穿线孔，一面刻有贯通上、下的十等分线. 用该衡杆称物，可以把被称物与砝码放在提纽两边不同位置的刻线上，这样，用同一个砝码就可以称出大于它一倍或几倍重量的物体. 如图为铜衡杆的使用示意图，此时被称物质量是砝码质量的________倍.

答案： 1.2解析：由题意，得$5m_{被称物}=6m_{砝码}$。$\therefore m_{被称物}:m_{砝码}=6:5 = 1.2$。

13. [新考向]小慧同学在学习了八年级下册“9.1成比例线段”一课后，发现学习内容是一个逐步特殊化的过程，请在横线上填写适当的数值，感受这种特殊化的学习过程.
$\frac{a}{x}=\frac{y}{c}$ $\xrightarrow{当x = y = b时}$ $\frac{a}{b}=\frac{b}{c}$ $\xrightarrow{当\frac{a}{c}=}$ 出现比例中项线段
$\frac{a}{b}=\frac{b}{c}=\sqrt{2}$ 出现特殊线段比

答案： 2解析：$\because\frac{a}{b}=\frac{b}{c}=\sqrt{2}$，$\therefore a = \sqrt{2}b$，$b = \sqrt{2}c$，$\therefore a = 2c$，$\therefore\frac{a}{c}=2$，即当$\frac{a}{c}=2$时，$\frac{a}{b}=\frac{b}{c}=\sqrt{2}$。

14. 求下列各式中x的值.
（1）$\frac{-3}{x}=\frac{2}{-6}$；
（2）x：(x + 1) = (1 - x)：3.

答案： 解：
(1)$\because\frac{-3}{x}=\frac{2}{-6}$，$\therefore 2x = (-3)\times(-6)$，$\therefore x = 9$。
@@解：
(2)$\because x:(x + 1)=(1 - x):3$，$\therefore(x + 1)(1 - x)=3x$，整理，得$x^{2}+3x - 1 = 0$，解得$x=\frac{-3\pm\sqrt{13}}{2}$。

15. 如图，在Rt△ABC中，CD是斜边AB上的高线. 找出一组比例线段，并说明理由.

答案： 解：$AC$，$CD$，$AB$，$BC$是一组比例线段。理由如下：$\because$在$Rt\triangle ABC$中，$CD$是斜边$AB$上的高线，$\therefore S_{\triangle ABC}=\frac{1}{2}AC\times BC=\frac{1}{2}CD\times AB$，$\therefore AC\times BC = CD\times AB$，$\therefore\frac{AC}{CD}=\frac{AB}{BC}$，$\therefore AC$，$CD$，$AB$，$BC$是一组比例线段。

16. 如图，已知$\frac{AP}{AB}=\frac{PQ}{PB}=\frac{1}{3}$，且PQ = 2 cm. 求AB的长.

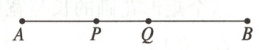
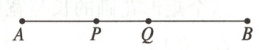
答案： 解：$\because\frac{PQ}{PB}=\frac{1}{3}$，$PQ = 2\ cm$，$\therefore PB = 3PQ = 6\ cm$。$\because\frac{AP}{AB}=\frac{1}{3}$，$\therefore AB = 3AP$，$\therefore AP + BP = 3AP$，即$AP + 6 = 3AP$，解得$AP = 3$，$\therefore AB = 9\ cm$，即$AB$的长为$9\ cm$。

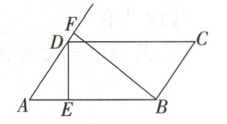
17. [推理能力]如图，在平行四边形ABCD中，DE⊥AB于点E，BF⊥AD于点F.
（1）AB，BC，BF，DE这四条线段能否成比例？如果不能，请说明理由；如果能，请写出比例式；
（2）若AB = 10，DE = 2.5，BF = 5，求BC的长.

答案： 解：
(1)$AB$，$BC$，$BF$，$DE$这四条线段能成比例，理由：$\because$在$\square ABCD$中，$DE\perp AB$，$BF\perp AD$，$AD = BC$，$\therefore S_{\square ABCD}=AB\cdot DE = AD\cdot BF$，$\therefore\frac{AD}{DE}=\frac{AB}{BF}$，即$AB$，$BC$，$BF$，$DE$这四条线段能成比例。
(2)由
(1)，得$AB\cdot DE = AD\cdot BF$，$\therefore 10\times2.5 = 5AD$，解得$AD = 5$。$\because$四边形$ABCD$是平行四边形，$\therefore BC = AD = 5$。