《2025年正大图书练测考八年级数学下册鲁教版》

11.矩形一个角的平分线分矩形一边为2 cm和3 cm两部分，则这个矩形的面积为（ ）
A.10 cm²
B.15 cm²
C.12 cm²
D.10 cm²或15 cm²

答案： D

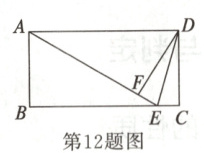
12.如图，在矩形ABCD中，AD = 4，AB = 2，在BC上取一点E，使AD = AE，过D作DF⊥AE于F，连接DE.下列结论不正确的是（ ）

A.△ADF≌△EAB
B.DE平分∠FDC
C.∠AEC = 150°
D.DF = $\frac{1}{2}$AF

答案： D

13.（2024·济南槐荫区期末）如图，在矩形ABCD中，点E为BA延长线上一点，F为CE的中点，以B为圆心，BF长为半径的圆弧过AD与CE的交点G，连接BG.若AB = 4，CE = 10，则AG = ________.

答案： 3
解析：
∵CE = 10，F为CE的中点，
∴CF = FE = 5.
∵四边形ABCD是矩形，
∴∠ABC = 90°，
∴BG = FB = FC = 5.
在Rt△ABG中，AG = $\sqrt{BG^{2}-AB^{2}}=\sqrt{5^{2}-4^{2}} = 3$.

14.如图，将矩形ABCD沿AE折叠，使点D落在边BC的点F处，已知AB = 6 cm，BC = 10 cm，则EC的长为________cm.

答案： $\frac{8}{3}$

15.（2024·云南）如图，在四边形ABCD中，点E，F，G，H分别是各边的中点，且AB//CD，AD//BC，四边形EFGH是矩形.
（1）求证：四边形ABCD是菱形；
（2）若矩形EFGH的周长为22，四边形ABCD的面积为10，求AB的长.

答案：

(1)证明：
如图，连接AC，BD交于点O，AC交FG于点N，BD交HG于点M，
∵AB//CD，AD//BC，
∴四边形ABCD是平行四边形.
∵四边形EFGH是矩形，
∴∠HGF = 90°.
∵点H，G分别是AD，DC的中点，
∴HG//AC，HG = $\frac{1}{2}AC$，
∴∠HGF = ∠GNC，
∴∠GNC = 90°.
∵点G，F分别是DC，BC的中点，
∴GF//BD，GF = $\frac{1}{2}BD$，
∴∠GNC = ∠MOC = 90°，
∴BD⊥AC，
∴四边形ABCD是菱形.
(2)解：
∵矩形EFGH的周长为22，
∴HG + FG = 11，
∴AC + BD = 22.
∵$\frac{1}{2}×AC×BD = 10$，
∴AC×BD = 20.
∵(AC + BD)² = AC² + 2×AC×BD + BD²，
∴AC² + BD² = 444，
∴$\frac{1}{4}AC^{2}+\frac{1}{4}BD^{2}=111$，
∴AO² + BO² = 111，
∴AB² = AO² + BO² = 111，
∴AB = $\sqrt{111}$.

16.（2024·淄博周村区期末）如图，在矩形ABCD中，AD = 4，AB = 6，对角线AC，BD交于点O，点E，F分别是CD，DA延长线上的点，且DE = 3，AF = 2，连接EF，点G为EF的中点.连接OE，交AD于点H，连接GH.
（1）猜想：H是OE的中点吗？并加以证明；
（2）求GH的长.

答案：
解：
(1)H是OE的中点.
证明：取AD的中点M，连接OM，如图1，

∵四边形ABCD是矩形，对角线AC，BD交于点O，
∴点O是AC的中点.
∵点M是AD的中点，
∴CD//OM，OM = $\frac{1}{2}CD=\frac{1}{2}AB = 3 = DE$，
∴∠MOH = ∠DEH.
∵∠OHM = ∠EHD，
∴△OHM≌△EHD(AAS)，
∴OH = EH，即H是OE的中点.
(2)连接OF，如图2，

∵点M是AD的中点，
∴AM = $\frac{1}{2}AD = 2$，
∴FM = FA + AM = 2 + 2 = 4.
∵OM//CD，
∴∠FMO = ∠ADC = 90°，
∴FO = $\sqrt{FM^{2}+MO^{2}}=\sqrt{4^{2}+3^{2}} = 5$.
∵点G是EF的中点，点H是OE的中点，
∴GH = $\frac{1}{2}FO=\frac{5}{2}$.