第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
12. 如图,在菱形ABCD中,AB = 5 cm,∠ADC = 120°,点E,F同时由A,C两点出发,分别沿AB,CB方向,向点B匀速移动(到点B为止),点E的速度为1 cm/s,点F的速度为2 cm/s,经过t s △DEF为等边三角形,则t的值为( )

A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{3}{2}$
D. $\frac{5}{3}$

A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{3}{2}$
D. $\frac{5}{3}$
答案:
D 解析:连接 BD,
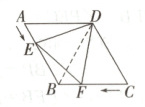
∵四边形 ABCD 是菱形,
∴AB = AD,∠ADB = $\frac{1}{2}$∠ADC = 60°,
∴△ABD 是等边三角形,
∴AD = BD。
又
∵△DEF 是等边三角形,
∴∠EDF = ∠DEF = 60°,DE = DF。
又
∵∠ADB = 60°,
∴∠ADE = ∠BDF。
在△ADE 和△BDF 中,
$\begin{cases}DE = DF \\\angle ADE = \angle BDF \\AD = BD\end{cases}$
∴△ADE≌△BDF(SAS),
∴AE = BF。
∵AE = t,CF = 2t,
∴BF = BC - CF = 5 - 2t,
∴t = 5 - 2t,
∴t = $\frac{5}{3}$。故选 D。
D 解析:连接 BD,

∵四边形 ABCD 是菱形,
∴AB = AD,∠ADB = $\frac{1}{2}$∠ADC = 60°,
∴△ABD 是等边三角形,
∴AD = BD。
又
∵△DEF 是等边三角形,
∴∠EDF = ∠DEF = 60°,DE = DF。
又
∵∠ADB = 60°,
∴∠ADE = ∠BDF。
在△ADE 和△BDF 中,
$\begin{cases}DE = DF \\\angle ADE = \angle BDF \\AD = BD\end{cases}$
∴△ADE≌△BDF(SAS),
∴AE = BF。
∵AE = t,CF = 2t,
∴BF = BC - CF = 5 - 2t,
∴t = 5 - 2t,
∴t = $\frac{5}{3}$。故选 D。
13. 已知:如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为________。


答案:
(3,4)或(2,4)或(8,4) 解析:
∵D 是 OA 的中点,
∴OD = AD = $\frac{1}{2}$OA = 5。
(1)当 OP = OD = 5 时,
∵CO = 4,
∴CP = $\sqrt{OP^{2}-OC^{2}}$ = 3,
∴P(3,4)。
(2)如图,当 OD = PD = 5 时,
过点 D 作 DN⊥BC 于点 N,则四边形 OCND 为矩形,
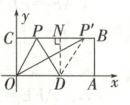
DN = OC = 4,DO = NC = 5,
∴PN = $\sqrt{DP^{2}-DN^{2}}$ = 3,
从而 CP = CN - PN = 5 - 3 = 2 或 CP′ = CN + P′N = 5 + 3 = 8,
∴P(2,4)或(8,4)。
(3)当 OP = PD 时,P($\frac{5}{2}$,4),
此时腰长为$\sqrt{(\frac{5}{2})^{2}+4^{2}}$ ≠ 5,故这种情况不合题意,舍去。
故点 P 的坐标为(3,4)或(2,4)或(8,4)。
(3,4)或(2,4)或(8,4) 解析:
∵D 是 OA 的中点,
∴OD = AD = $\frac{1}{2}$OA = 5。
(1)当 OP = OD = 5 时,
∵CO = 4,
∴CP = $\sqrt{OP^{2}-OC^{2}}$ = 3,
∴P(3,4)。
(2)如图,当 OD = PD = 5 时,
过点 D 作 DN⊥BC 于点 N,则四边形 OCND 为矩形,

DN = OC = 4,DO = NC = 5,
∴PN = $\sqrt{DP^{2}-DN^{2}}$ = 3,
从而 CP = CN - PN = 5 - 3 = 2 或 CP′ = CN + P′N = 5 + 3 = 8,
∴P(2,4)或(8,4)。
(3)当 OP = PD 时,P($\frac{5}{2}$,4),
此时腰长为$\sqrt{(\frac{5}{2})^{2}+4^{2}}$ ≠ 5,故这种情况不合题意,舍去。
故点 P 的坐标为(3,4)或(2,4)或(8,4)。
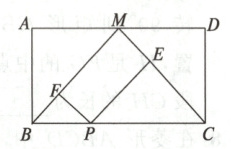
14. 如图,在矩形ABCD中,点M是边AD的中点,点P是边BC上的动点,PE⊥MC,PF⊥BM,垂足为点E,F。
(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?证明你的结论;
(2)如果四边形PEMF为矩形,那么当点P运动到什么位置时,矩形PEMF变为正方形?证明你的猜想。
(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?证明你的结论;
(2)如果四边形PEMF为矩形,那么当点P运动到什么位置时,矩形PEMF变为正方形?证明你的猜想。

答案:
解:
(1)当 AD = 2AB 时,四边形 PEMF 为矩形。
证明:
∵四边形 ABCD 为矩形,
∴∠A = ∠D = 90°。
∵点 M 是边 AD 的中点,
∴AM = DM = $\frac{1}{2}$AD。
∵AD = 2AB = 2CD,
∴AB = AM = DM = CD,
∴∠ABM = ∠AMB = 45°,∠DCM = ∠DMC = 45°,
∴∠BMC = 180° - 45° - 45° = 90°。
∵PE⊥MC,PF⊥BM,
∴∠MEP = ∠PFM = 90°,
∴四边形 PEMF 为矩形,
即当 AD = 2AB 时,四边形 PEMF 为矩形。
(2)当 P 是 BC 的中点时,矩形 PEMF 变为正方形。
证明:
∵四边形 PEMF 为矩形,
∴∠PFM = ∠PFB = ∠PEC = 90°。
由
(1)知∠FBP = ∠ECP = 45°。
在△BFP 和△CEP 中,
$\begin{cases}\angle FBP = \angle ECP \\\angle PFB = \angle PEC \\BP = CP\end{cases}$
∴△BFP≌△CEP(AAS),
∴PF = PE。
又
∵四边形 PEMF 是矩形,
∴矩形 PEMF 是正方形,
即当 P 是 BC 的中点时,矩形 PEMF 为正方形。
(1)当 AD = 2AB 时,四边形 PEMF 为矩形。
证明:
∵四边形 ABCD 为矩形,
∴∠A = ∠D = 90°。
∵点 M 是边 AD 的中点,
∴AM = DM = $\frac{1}{2}$AD。
∵AD = 2AB = 2CD,
∴AB = AM = DM = CD,
∴∠ABM = ∠AMB = 45°,∠DCM = ∠DMC = 45°,
∴∠BMC = 180° - 45° - 45° = 90°。
∵PE⊥MC,PF⊥BM,
∴∠MEP = ∠PFM = 90°,
∴四边形 PEMF 为矩形,
即当 AD = 2AB 时,四边形 PEMF 为矩形。
(2)当 P 是 BC 的中点时,矩形 PEMF 变为正方形。
证明:
∵四边形 PEMF 为矩形,
∴∠PFM = ∠PFB = ∠PEC = 90°。
由
(1)知∠FBP = ∠ECP = 45°。
在△BFP 和△CEP 中,
$\begin{cases}\angle FBP = \angle ECP \\\angle PFB = \angle PEC \\BP = CP\end{cases}$
∴△BFP≌△CEP(AAS),
∴PF = PE。
又
∵四边形 PEMF 是矩形,
∴矩形 PEMF 是正方形,
即当 P 是 BC 的中点时,矩形 PEMF 为正方形。
15. [教材P29复习题T13变式]如图所示,在直角梯形ABCD中,AD//BC,∠A = 90°,AB = 12,BC = 20,AD = 16. 动点P从点B出发,沿射线BC的方向以每秒2个单位长度的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长度的速度向点D运动,当其中一个动点到达端点时停止运动,另一个动点也随之停止运动。设运动的时间为t秒。
(1)设△DPQ的面积为S,用含t的式子表示S;
(2)当t为何值时,四边形PCDQ是平行四边形?
(3)当t为何值时,PQ = PD?
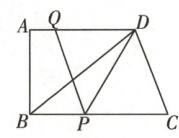
(1)设△DPQ的面积为S,用含t的式子表示S;
(2)当t为何值时,四边形PCDQ是平行四边形?
(3)当t为何值时,PQ = PD?

答案:
解:
(1)由题意,得 AQ = t,则 DQ = 16 - t,
∵AD//BC,AB = 12,
∴△DPQ 的面积为 S = $\frac{1}{2}$(16 - t)×12 = - 6t + 96(0<t≤10)。
(2)
∵AD//BC,
∴当 DQ = PC 时,四边形 PCDQ 是平行四边形。
∵BP = 2t,
∴PC = 20 - 2t,
∴16 - t = 20 - 2t,解得 t = 4,
∴当 t = 4 时,四边形 PCDQ 是平行四边形。
(3)如图,过点 P 作 PH⊥AD 于 H,
则四边形 ABPH 为矩形,
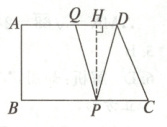
∴AH = BP = 2t。
当 PQ = PD 时,
∵PH⊥AD,
∴QH = HD = $\frac{1}{2}$(16 - t),
∴t + $\frac{1}{2}$(16 - t) = 2t,解得 t = $\frac{16}{3}$,
∴当 t = $\frac{16}{3}$时,PQ = PD。
解:
(1)由题意,得 AQ = t,则 DQ = 16 - t,
∵AD//BC,AB = 12,
∴△DPQ 的面积为 S = $\frac{1}{2}$(16 - t)×12 = - 6t + 96(0<t≤10)。
(2)
∵AD//BC,
∴当 DQ = PC 时,四边形 PCDQ 是平行四边形。
∵BP = 2t,
∴PC = 20 - 2t,
∴16 - t = 20 - 2t,解得 t = 4,
∴当 t = 4 时,四边形 PCDQ 是平行四边形。
(3)如图,过点 P 作 PH⊥AD 于 H,
则四边形 ABPH 为矩形,

∴AH = BP = 2t。
当 PQ = PD 时,
∵PH⊥AD,
∴QH = HD = $\frac{1}{2}$(16 - t),
∴t + $\frac{1}{2}$(16 - t) = 2t,解得 t = $\frac{16}{3}$,
∴当 t = $\frac{16}{3}$时,PQ = PD。
查看更多完整答案,请扫码查看


