《2025年正大图书练测考八年级数学下册鲁教版》

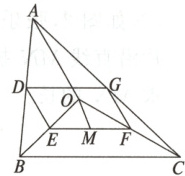
7. 如图，点O是△ABC内一点，连接OA，OB，OC，并将AB，OB，OC，AC的中点D，E，F，G依次连接，得到四边形DEFG.
（1）求证：四边形DEFG是平行四边形；
（2）若BO⊥CO，M为EF的中点，且OA = 8，OM = 3，求四边形DEFG的周长.

答案：
(1)证明：
∵D，G分别是AB，AC的中点，
∴DG//BC，DG = 1/2BC.
∵E，F分别是OB，OC的中点，
∴EF//BC，EF = 1/2BC，
∴DG = EF，DG//EF，
∴四边形DEFG是平行四边形.
(2)解：
∵BO⊥CO，M为EF的中点，OM = 3，
∴EF = 2OM = 6.
由
(1)知四边形DEFG是平行四边形，
∴DG = EF = 6.
∵D是AB的中点，E是BO的中点，
∴DE = 1/2AO = 4，
∴四边形DEFG的周长为4 + 4 + 6 + 6 = 20.

8.（2024·北京海淀区校级期中）如图，E，F，G，H分别是边长为4的正方形ABCD四条边上的点（不与顶点重合），且满足AE = DH = CG = BF，记AF = x，则下列四个变量中，不存在最小值的是（ ）

A. BF
B. FE
C. FH
D. $S_{四边形EFGH}$

答案： A 解析：
∵四边形ABCD是正方形，
∴AB = BC = CD = AD，∠A = ∠B = ∠C = ∠D = 90°.
∵AE = DH = CG = BF，
∴DE = AF = BG = CH，
∴△AEF≌△BFG(SAS)，
同理可得△BFG≌△CGH(SAS)，△CGH≌△DHE(SAS)，
∴EF = FG = GH = EH，∠AFE = ∠FGB，
∴四边形EFGH是菱形.
∵∠BFG + ∠BGF = 90°，
∴∠AFE + ∠BFG = 90°，
∴∠EFG = 90°，
∴四边形EFGH是正方形，
∴FH = √2EF，S四边形EFGH = EF².
∵EF² = AE² + AF² = AE² + (4 - AE)² = 2(AE - 2)² + 8，
∴当AE = 2时，EF有最小值，S四边形EFGH有最小值，
∴HF有最小值.
故选A.

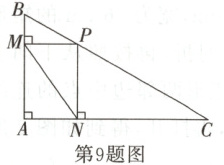
9.（2024·恩施期中）如图，在Rt△ABC中，∠BAC = 90°，AB = 5，AC = 12，点P是BC边上的一个动点，PM⊥AB于点M，PN⊥AC于点N，则MN的最小值为________.

答案：
60/13
解析：在Rt△ABC中，∠BAC = 90°，AB = 5，AC = 12，
∴BC = √(AB² + AC²) = 13.
∵PM⊥AB于点M，PN⊥AC于点N，∠BAC = 90°，
∴四边形AMPN为矩形.
如图，连接AP，则MN = AP，
∴AP最小时，MN最小.
∵垂线段最短，
∴当AP⊥BC时，AP最小.
∵S△ABC = 1/2AB·AC = 1/2BC·AP，
∴5×12 = 13AP，
∴AP = 60/13，
∴MN的最小值为60/13.

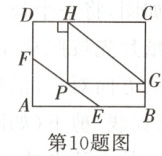
10. 如图，在矩形ABCD中，E，F分别是边AB，AD上的动点，P是线段EF的中点，PG⊥BC，PH⊥CD，G，H为垂足，连接GH. 若AB = 4，AD = 3，EF = 3，则线段GH长度的最小值是________.

答案： 7/2

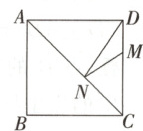
11. 如图，正方形ABCD的边长为5，M在DC上，且DM = 2，N是AC上的一动点，求DN + MN的最小值.

答案：
解：
∵四边形ABCD是正方形，
∴点B关于AC的对称点为点D，
如图，连接BM交AC于点N，则此时DN + MN的值最小，
∴DN + MN = BN + MN = BM.
∵CD = BC = 5，DM = 2，
∴MC = 3，
∴BM = √(3² + 5²) = √34.